什么是注意力机制?注意力机制的计算规则
我们观察事物时,之所以能够快速判断一种事物(当然允许判断是错误的),是因为我们大脑能够很快把注意力放在事物最具有辨识度的部分从而作出判断,而并非是从头到尾的观察一遍事物后,才能有判断结果,正是基于这样的理论,就产生了注意力机制。
什么是注意力计算规则:
它需要三个指定的输入Q(query),K(key),V(value),然后通过计算公式得到注意力的结果,这个结果代表query在key和value作用下的注意力表示.当输入的Q=K=V时,称作自注意力计算规则。
常见的注意力计算规则:
|| ·将Q,K进行纵轴拼接,做一次线性变化,再使用softmax处理获得结果最后与V做张量乘法。
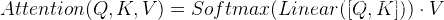
|| ·将Q,K进行纵轴拼接,做一次线性变化后再使用tanh函数激活,然后再进行内部求和,最后使用softmax处理获得结果再与V做张量乘法.
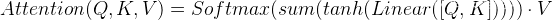
|| ·将Q与K的转置做点积运算,然后除以一个缩放系数再使用softmax处理获得结果最后与V做张量乘法。
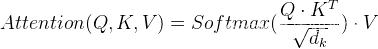
说明:当注意力权重矩阵和V都是三维张量且第一维代表为batch条数时, 则做bmm运算.bmm是一种特殊的张量乘法运算。
bmm运算演示:
# 如果参数1形状是(b × n × m), 参数2形状是(b × m × p), 则输出为(b × n × p)
>>> input = torch.randn(10, 3, 4)
>>> mat2 = torch.randn(10, 4, 5)
>>> res = torch.bmm(input, mat2)
>>> res.size()
torch.Size([10, 3, 5])
注意力机制的作用
在解码器端的注意力机制:能够根据模型目标有效的聚焦编码器的输出结果,当其作为解码器的输入时提升效果,改善以往编码器输出是单一定长张量,无法存储过多信息的情况。
在编码器端的注意力机制:主要解决表征问题,相当于特征提取过程,得到输入的注意力表示。般使用自注意力(self-attention)。
注意力机制实现步骤
第一步:根据注意力计算规则,对Q,K,V进行相应的计算
第二步:根据第一步采用的计算方法,如果是拼接方法,则需要将Q与第二步的计算结果再进行拼接,如果是转置点积一般是自注意力,Q与V相同,则不需要进行与Q的拼接
第三步:最后为了使整个attention机制按照指定尺寸输出,使用线性层作用在第二步的结果上做个线性变换,得到最终对Q的注意力表示
常见注意力机制的代码分析:
import torch
import torch.nn as nn
import torch.nn.functional as F
class Attn(nn.Module):
def __init__(self, query_size, key_size, value_size1, value_size2, output_size):
"""初始化函数中的参数有5个, query_size代表query的最后一维大小
key_size代表key的最后一维大小, value_size1代表value的导数第二维大小,
value = (1, value_size1, value_size2)
value_size2代表value的倒数第一维大小, output_size输出的最后一维大小"""
super(Attn, self).__init__()
# 将以下参数传入类中
self.query_size = query_size
self.key_size = key_size
self.value_size1 = value_size1
self.value_size2 = value_size2
self.output_size = output_size
# 初始化注意力机制实现第一步中需要的线性层.
self.attn = nn.Linear(self.query_size + self.key_size, value_size1)
# 初始化注意力机制实现第三步中需要的线性层.
self.attn_combine = nn.Linear(self.query_size + value_size2, output_size)
def forward(self, Q, K, V):
"""forward函数的输入参数有三个, 分别是Q, K, V, 根据模型训练常识, 输入给Attion机制的
张量一般情况都是三维张量, 因此这里也假设Q, K, V都是三维张量"""
# 第一步, 按照计算规则进行计算,
# 我们采用常见的第一种计算规则
# 将Q,K进行纵轴拼接, 做一次线性变化, 最后使用softmax处理获得结果
attn_weights = F.softmax(
self.attn(torch.cat((Q[0], K[0]), 1)), dim=1)
# 然后进行第一步的后半部分, 将得到的权重矩阵与V做矩阵乘法计算,
# 当二者都是三维张量且第一维代表为batch条数时, 则做bmm运算
attn_applied = torch.bmm(attn_weights.unsqueeze(0), V)
# 之后进行第二步, 通过取[0]是用来降维, 根据第一步采用的计算方法,
# 需要将Q与第一步的计算结果再进行拼接
output = torch.cat((Q[0], attn_applied[0]), 1)
# 最后是第三步, 使用线性层作用在第三步的结果上做一个线性变换并扩展维度,得到输出
# 因为要保证输出也是三维张量, 因此使用unsqueeze(0)扩展维度
output = self.attn_combine(output).unsqueeze(0)
return output, attn_weights
调用:
query_size = 32
key_size = 32
value_size1 = 32
value_size2 = 64
output_size = 64
attn = Attn(query_size, key_size, value_size1, value_size2, output_size)
Q = torch.randn(1,1,32)
K = torch.randn(1,1,32)
V = torch.randn(1,32,64)
out = attn(Q, K ,V)
print(out[0])
print(out[1])
输出效果:
tensor([[[ 0.4477, -0.0500, -0.2277, -0.3168, -8.4096, -0.5982, 0.1548,
-8.8771, -8.0951. 8.1833. 8.3128. 8.1260, 8.4420. 8.8495.
-0.7774, -0.0995, 0.2629, 0.4957, 1.0922, 0.1428, 0.3024.
-0.2646, -0.0265, 0.0632, 0.3951, 0.1583, 0.1130, 0.5500,
-0.1887, -0.2816, -0.3800, -0.5741, 0.1342, 0.0244, -0.2217,
0.1544, 0.1865, -0.2019, 0.4090, -0.4762, 0.3677, -0.2553,
-0.5199, 0.2290, -0.4407, 0.0663, -8.0182, -8.2168, 0.0913,
-0.2340, 0.1924, -0.3687, 0.1508, 0.3618, -0.0113, 0.2864.
-0.1929, -0.6821, 0.0951, 0.1335, 0.3560, -0.3215
,0.6461,
0.1532]]],grad_fn=<UnsqueezeBackward0>)
tensor([[0.0395, 0.0342, 0.0200, 0.0471, 0.0177, 0.0209, 0.0244, 0.0465, 0.0346,
0.0378, 0.0282, 0.0214, 0.0135, 0.0419, 0.0926, 0.0123, 0.0177, 0.0187,
0.0166, 0.8225, 0.0234, 0.0284, 0.0151, 0.0239, 0.0132, 0.0439, 0.0507,
0.0419, 8.0352, 8.0392, 8.0546, 0.0224]], grad_fn=<SoftmaxBackward>)