
广义增量规则的公式
- 对于单层神经网络的增量规则,已经过时啦,现在存在一种更广义的增量规则形式。对于任意激活函数,增量规则表示如下式
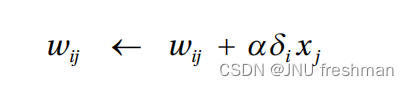
- 它与前一节的delta规则相同,只是ei被替换为δi。在这个方程中,δi被定义为:
-
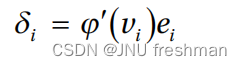
ei =输出节点i
vi =输出节点i的加权和
φ‘=输出节点i的激活函数φ的导数
s型函数的增量规则
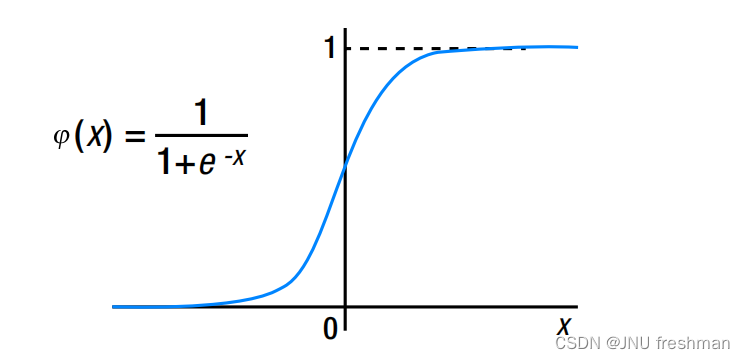
对于该函数进行求导
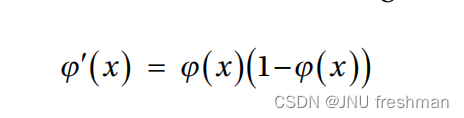
代入公式:
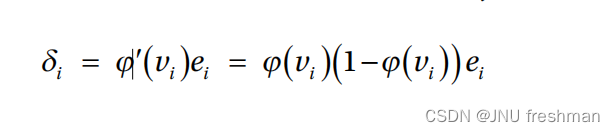
最后,我们可以得到s型函数的增量规则:
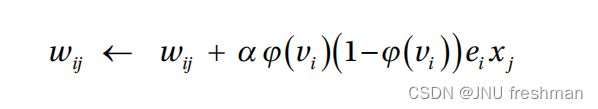
虽然权值更新公式相当复杂,但它保持了相同的基本概念,即权值是根据输出节点误差ei和输入节点值xj的比例来确定的