GM(1,1)应用案例1
北方某城市1986-1992年道路交通平均噪声级数数据如表(1)建立GM(1,1)模型。
表(1)城市交通平均噪声级数数据/db(A)
| 编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 年份 |
1986 |
1987 |
1988 |
1989 |
1990 |
1991 |
1992 |
| Leq |
71.1 |
72.4 |
72.4 |
72.1 |
71.4 |
72.0 |
71.6 |
【符号设置】
- x(0)(k) 原始数据,k=1,2,…,7
- x(1)(k) 累加生成数列(1-AGO)列,k=1,2,…,7
- z(1)(k) (1-AGO)序列的均值,k=2,3,…,7
- λ(k) 级比数据,k=2,3,…,7
- a,b 待拟合参数
【建立模型】
1、级比检验
原始数据为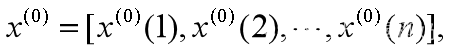
= [71.1 72.4 72.4 72.1 71.4 72.0 71.6],根据级比公式
计算级比为λ=[0.9820 1.0000 1.0042 1.0098 0.9917 1.0056],级比容差范围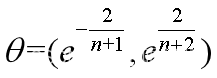 =[0.7788 1.2840]
=[0.7788 1.2840]
λ每个分量都在容差范围,即原始数据可以作GM(1,1)建模。
λ和容差计算程序:
x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6];
n=length(x0);
lamuda=x0(1:n-1)./x0(2:n);
xita=exp([-2/(n+1),2/(n+1)]);
lamudamm=minmax(lamuda);
[lamudamm;xita]
2、GM(1,1)建模
(2.1) 对原始数据x(0)作一次(阶)累加.
公式为
计算得到x(1)=[71.1 143.5 215.9 288.0 359.4 431.4 503.],
(2.2)对x(1)取均值(作一次平滑)
公式为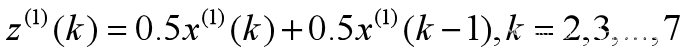
计算得到z(1)=[107.3 179.7 251.95 323.7 395.4 467.2]
(2.3)构造数据矩阵B和数据向量Y
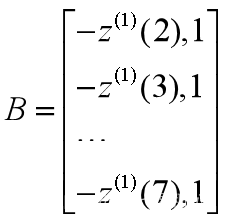
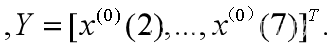
(2.4)计算最小二乘参数

经计算得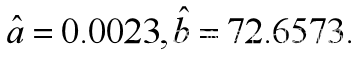
代码如下:
x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6];
n=length(x0);
x1=cumsum(x0);
z=(x1(1:n-1)+x1(2:n))/2;
B=[z',ones(n-1,1)];Y=(x0(2:n))';
u=inv(B'*B)*B'*Y;
(2.5)建立模型
白化方程 求解,得
求解,得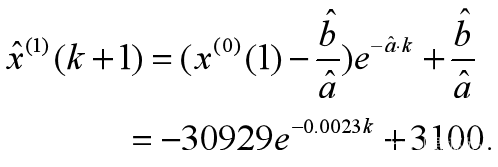 【6】
【6】
(2.6)求生成序列预测值和原始数据还原值
累加数据的预测公式为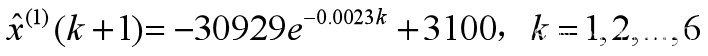
取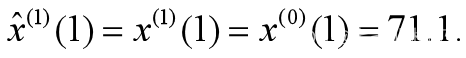 则原始数据的预测公式为
则原始数据的预测公式为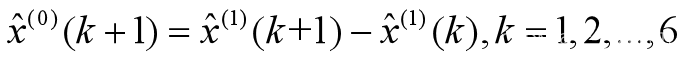 【7】
【7】
3、模型检验
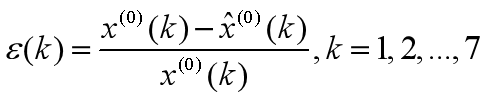 【8】
【8】
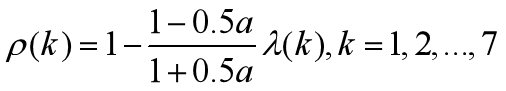 【9】
【9】
根据公式[8]和[9],计算残差和级比偏差,相关计算结果填入表2
GM(1,1)所有计算及检验计算程序
x0=[71.1 72.4 72.4 72.1 71.4 72.0 71.6];
n=length(x0);
lamuda=x0(1:n-1)./x0(2:n);
x1=cumsum(x0);
z=(x1(1:n-1)+x1(2:n))/2;
B=[-z',ones(n-1,1)];Y=(x0(2:n))';
u=inv(B'*B)*B'*Y;
x1(1)=x0(1);
x2(1)=x0(1);
xy(1)=x0(1);
for k=1:n-1
x2(k+1)=(x0(1)-u(2)/u(1))*exp(-u(1)*k)+u(2)/u(1);
end
xy=[x0(1),diff(x2)];
err=x0-xy;
errb=err./x0;
a=u(1);
rho=(1-(1-0.5*a)/(1+0.5*a))*lamuda;
[x0',x1',[0,z]',xy',err',errb',[0,rho]']
表2 GM(1,1)模型残差与级比偏差
| 原始 数据 |
累加 数据 |
均值 数据 |
x0预测 |
残差 |
相对 误差 |
级比 偏差 |
| 71.1 |
71.1 |
0 |
71.1 |
0 |
0 |
0 |
| 72.4 |
143.5 |
107.3 |
72.40574 |
-0.00574 |
-7.9E-05 |
0.002299 |
| 72.4 |
215.9 |
179.7 |
72.23624 |
0.163763 |
0.002262 |
0.002341 |
| 72.1 |
288 |
251.95 |
72.06713 |
0.032871 |
0.000456 |
0.002351 |
| 71.4 |
359.4 |
323.7 |
71.89842 |
-0.49842 |
-0.00698 |
0.002364 |
| 72 |
431.4 |
395.4 |
71.7301 |
0.269901 |
0.003749 |
0.002322 |
| 71.6 |
503 |
467.2 |
71.56218 |
0.037824 |
0.000528 |
0.002354 |
由表2可以得到,残差百分比和级比偏差都小于0.1,预测达到较高要求