基于Python实现的默克尔树

       默克尔树常见的结构是二叉树，但它也可以是多叉树，它具有树结构的全部特点。 默克尔树的基础数据不是固定的，想存什么数据都可以，因为它只要数据经过哈希运算得到的哈希值。 默克尔树是从下往上逐层计算，每个中间节点是根据相邻的两个叶子节点组合计算得出的，而根节点是根据两个中间节点组合计算得出的，所以叶节点是基础。因此，底层数据的任何变动，都会传递到其父节点，一直到树的根节点。

      默克尔树是区块链技术中用于保障数据不被篡改的重要安全手段之一，有着非常重要的作用。以下例子演示了通过遍历的方式构建默克尔树，并计算和显示每个步骤的哈希值。

import hashlib #用于哈希值计算
#默克尔树节点类的定义
class MerkleNode(object):
    def __init__(self,left=None,right=None,data=None):
        self.left = left
        self.right = right
        # data中保存着哈希值
        self.data = data

#以递归的方式构建默克尔树
def createTree(nodes):
    list_len = len(nodes)
    if list_len == 0:
        return 0
    else:
        while list_len %2 != 0:
            nodes.extend(nodes[-1:])
            list_len = len(nodes)
        secondary = []
        #两两合并节点，并计算其哈希值
        for k in [nodes[x:x+2] for x in range(0,list_len,2)]:
            d1 = k[0].data.encode()
            d2 = k[1].data.encode()
            md5 = hashlib.md5()
            md5.update(d1+d2)
            newdata = md5.hexdigest()           
            node = MerkleNode(left=k[0],right=k[1],data=newdata)
            secondary.append(node)
        if len(secondary) == 1:
            return secondary[0]
        else:
            return createTree(secondary)
        
#利用广度优先搜索算法对节点数据进行遍历
def BFS(root):
    print('开始广度优先搜索，构建默克尔树...')
    i=0
    queue = []
    queue.append(root)
    while(len(queue)>0):
        e = queue.pop(0)
        i+=1
        #print("Hash Value:"+str(i),e.data)
        if e.left != None:
            queue.append(e.left)
        if e.right != None:
            queue.append(e.right)
        print("Hash value:"+str(i),e.data)


if __name__ == "__main__":
    blocks = ['node1','node2','node3','node4'] #示例数据，包含4个节点
    nodes = [] #节点初始化
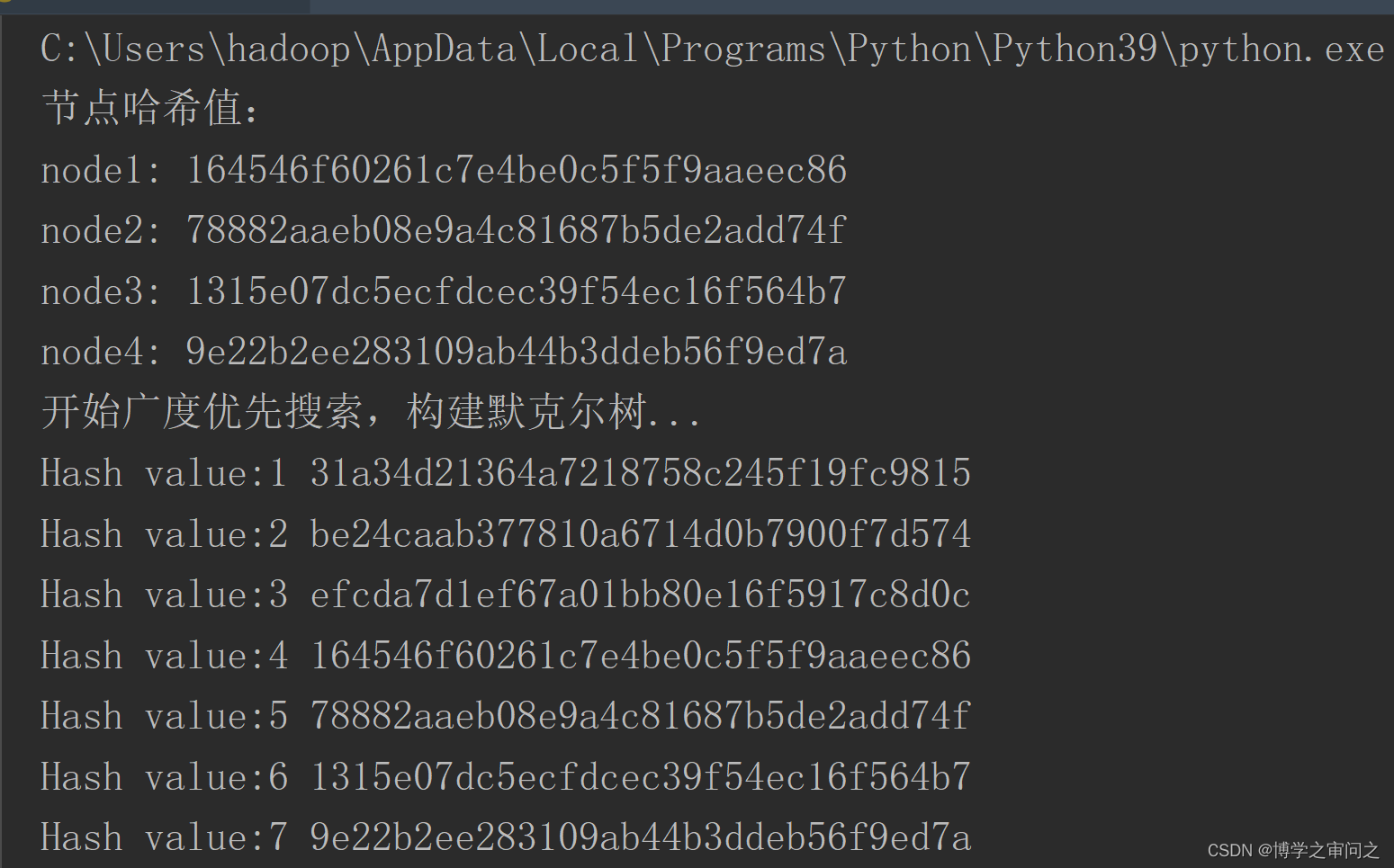
    print("节点哈希值：")
    for element in blocks: #遍历示例数据
        md5 = hashlib.md5() #摘要算法
        md5.update(element.encode())
        d=md5.hexdigest() #计算节点的信息摘要
        nodes.append(MerkleNode(data=d)) #添加至默克尔树节点中
        print(element+":",d)
    root = createTree(nodes) #创建默克尔根节点
    BFS(root) #基于BFS算法构建默克尔树并输出所有的哈希(摘要)

运行截图如下：