拍运算 信号中“拍”的概念 通信中“拍”的概念

我这有两个同方向但不同频率的谐振动 x 1 x_1 x1​ 和 x 2 x_2 x2​，可以用旋转矢量 A 1 boldsymbol{A}_1 A1​ 和 A 2 boldsymbol{A}_2 A2​ 来表示， x 1 x_1 x1​ 和 x 2 x_2 x2​ 就是旋转矢量在 $x$ 轴上的投影，
x 1 = A 1 cos ⁡ ( ω 1 t + φ 1 ) x 2 = A 2 cos ⁡ ( ω 2 t + φ 2 ) x_1=A_1cos(omega_1t+varphi_1) \ x_2=A_2cos(omega_2t+varphi_2) x1​=A1​cos(ω1​t+φ1​)x2​=A2​cos(ω2​t+φ2​)

A 1 boldsymbol{A}_1 A1​ 和 A 2 boldsymbol{A}_2 A2​ 的角速度不同，它们的合成矢量 $\mathbf{A}$ 不以恒定角速度旋转，这一点非常重要，这说明了他们的合成振动不再是谐振动。$\mathbf{A}$ 沿 $x$ 轴投影的振幅为，
A = A 1 2 + A 2 2 + 2 A 1 A 2 cos ⁡ ( ω 2 − ω 1 ) t A=sqrt{A_1^2+A_2^2+2A_1A_2cos(omega_2-omega_1)t} A=A12​+A22​+2A1​A2​cos(ω2​−ω1​)t ​

虽然它不是谐振动了，不再符合 A cos ⁡ ( ω t + φ ) Acos(omega_t+varphi) Acos(ωt​+φ) 的形式了，但它还是振动，只要是振动就有振幅的概念，并且振幅随时间周期性变化。

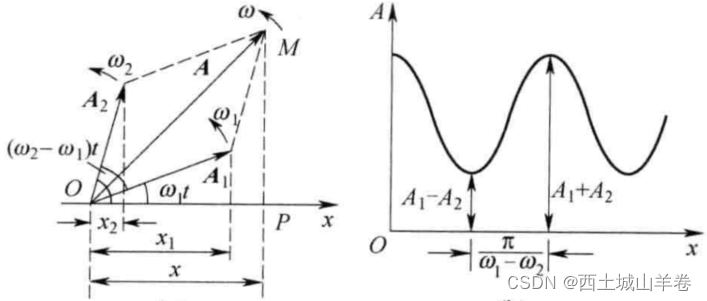
可以看出振幅在 A = A 1 + A 2 A=A_1+A_2 A=A1​+A2​ 和 A = ∣ A 1 − A 2 ∣ A=|A_1-A_2| A=∣A1​−A2​∣ 间周期性变化，振动频率为，
v = ∣ ω 2 − ω 1 ∣ 2 π v=frac{|omega_2-omega_1|}{2pi} v=2π∣ω2​−ω1​∣​

这里说的振动的频率是振幅从一次极大到另一次极大的变化，并不是说它是一个角频率为 ∣ ω 2 − ω 1 ∣ |omega_2-omega_1| ∣ω2​−ω1​∣ 的谐振动。因为它并非匀速变化的。

当两个谐振动的频率相差很小时，就会出现“拍”的现象。我这里有两个初相为零，频率差很小，振幅相同的谐振动，
x 1 = A 1 cos ⁡ ω 1 t x 2 = A 2 cos ⁡ ω 2 t x = x 1 + x 2 = [ 2 A 1 cos ⁡ 1 2 ( ω 2 − ω 1 ) t ] cos ⁡ 1 2 ( ω 2 + ω 1 ) t x_1=A_1cosomega_1t \ x_2=A_2cosomega_2t \ x=x_1+x_2=left[2A_1cosfrac{1}{2}(omega_2-omega_1)tright]cosfrac{1}{2}(omega_2+omega_1)t x1​=A1​cosω1​tx2​=A2​cosω2​tx=x1​+x2​=[2A1​cos21​(ω2​−ω1​)t]cos21​(ω2​+ω1​)t

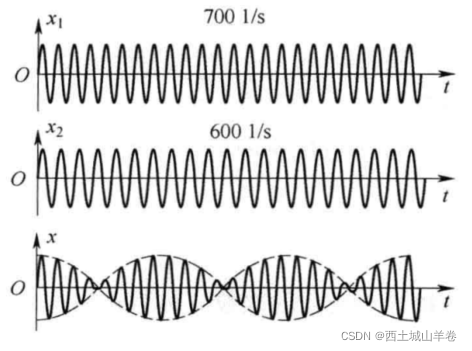
一定要明确，这里的合成信号已经不是一个谐振动了，它已经不再符合 A cos ⁡ ( ω t + φ ) Acos(omega_t+varphi) Acos(ωt​+φ) 的形式了，只不过 1 2 ( ω 2 + ω 1 ) frac{1}{2}(omega_2+omega_1) 21​(ω2​+ω1​) 是合成信号变化周期的主要原因。将 [ 2 A 1 cos ⁡ 1 2 ( ω 2 − ω 1 ) t ] left[2A_1cosfrac{1}{2}(omega_2-omega_1)tright] [2A1​cos21​(ω2​−ω1​)t] 部分视为合成信号的幅度，可以看出它是一个谐振动。所以我们能够感受到“拍”。

所谓“拍”，是从音乐的角度来讲的。两个频率相近的信号，我们认为音调几乎一样，他们两个的合成信号，音调提升一倍，但是能够明显的感受到音量的周期性涨落，这就是一“拍”。