相关性

        相关性分析是研究两组变量之间是否具有线性相关关系，所以做相关性分析的前提是假设变量之间存在线性相关性，得到的结果也是描述变量间的线性相关程度。除此之外，相关性分析方法还会有其他的假设条件。而灰色关联度分析首先对数据量要求很小，其次灰色关联度是通过判断变量的发展趋势的一致性决定相关性的大小，约束条件也小很多。

相关性分析的三种方法

        目前主要的相关性分析方法有皮尔逊相关系数、斯皮尔曼相关系数和肯达相关系数。

        其中皮尔逊相关系数和斯皮尔曼相关系数最为常用。皮尔逊相关系数虽然最经典，但是假设条件最多：

1、两组变量都服从正态分布

2、实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较大。

3、每组样本之间是独立抽样的。

4、总之，数据必须是连续型数据，服从正态分布，而且两组数据具有线性关系。

        所以，在做相关性分析时，最严谨的做法先要检验数据的分布特征，判断数据是否服从正态分布以及是否具有线性关系，当上面的条件都满足时，用皮尔逊相关系数最为有效，当有一个不满足时可以用斯皮尔曼相关系数，斯皮尔曼相关系数可以用于连续型也可以用于离散型数据，肯达相关系数适用于两个分类变量均为有序分类的情况，即两组数据都是离散型数据，所以使用的很少。

皮尔逊相关系数(pearson)：连续、正态、线性数据
肯达相关系数(kendall)：两组离散数据
斯皮尔曼相关系数(spearman)：适用范围广，只要数据满足单调关系，例如线性函数、指数函数、对数函数即可。

相关性分析代码

1、数据展示

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
datas=pd.read_excel(r'C:Users1003Desktop土地指标指标.xlsx')
datas=datas.iloc[:,:-2]
datas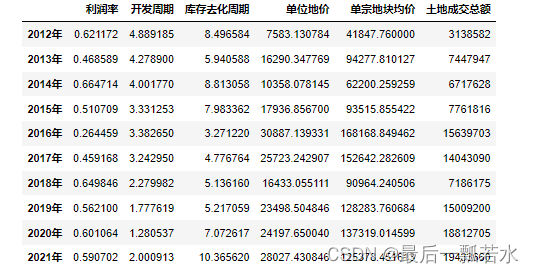

 2、标准化处理

这里对数据统一正向化处理。

from sklearn.preprocessing import MinMaxScaler
columns=datas.columns
standard_s2=MinMaxScaler()#创建StandardScaler()实例
datas=standard_s2.fit_transform(datas)#将DataFrame格式的数据按照每一个series分别标准化
datas=pd.DataFrame(datas,columns=columns)#将标准化后的数据改成DataFrame格式
datas

3、用pandas做相关性分析

pandas.DataFrame.corr(method='pearson')
'参数'
"""
method= pearson，kendall，spearman 对应着三种方法
默认meathod = pearson
"""

此处看看皮尔逊相关系数和斯皮尔曼相关系数的结果。

（1）、皮尔逊相关系数矩阵

#皮尔逊相关系数矩阵
datas.corr(method='spearman')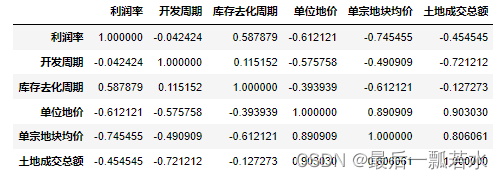

画热力图：

#热力图展示
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
sns.heatmap(round(datas.corr(method='pearson'), 2),cmap="YlGnBu")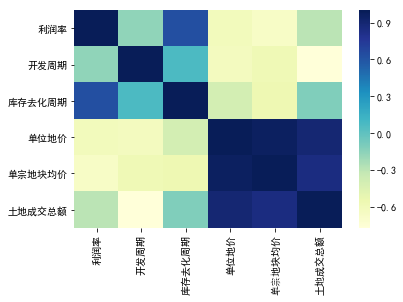

 （2）、斯皮尔曼相关系数矩阵

datas.corr(method='spearman')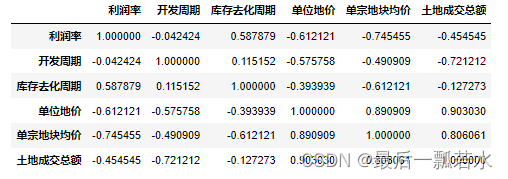

 画热力图：

plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
 # 设置展示一半，如果不需要注释掉mask即可
mask=np.zeros_like(round(datas.corr(method='spearman'), 2))
mask[np.triu_indices_from(mask)]=True
with sns.axes_style('white'):
    sns.heatmap(round(datas.corr(method='spearman'), 2),cmap="YlGnBu",annot=True,mask=mask)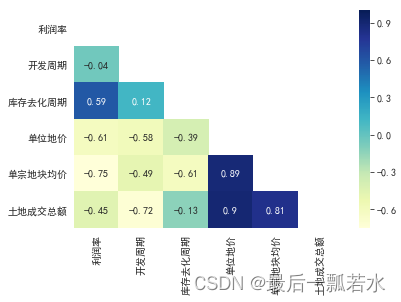

（下一篇用同样的数据做一下灰色关联度分析）