排序算法-合并排序法（MergeSort）

  排序算法-合并排序法（MergeSort）

1、说明

合并排序法（MergeSort）是针对已排序好的两个或两个以上的数列（或数据文件），通过合并的方式将其组合成一个大的且已排好序的数列（或数据文件），步骤如下：

1. 将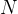个长度为1的键值成对地合并成个长度为2的键值组。
2. 将个长度为2的键值组成对地合并成个长度为4的键值组。
3. 将键值组不断地合并，直到合并成一组长度为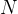的键值组为止。

2、算法分析

1. 合并排序法n个数据一般需要处理约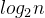次，每次处理的时间复杂度为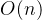，所以合并排序法的最好情况、最坏情况及平均情况的时间复杂度为。
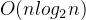2. 由于在排序过程中需要一个与数据文件大小同样的额外空间，故其空间复杂度为。
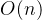3. 合并排序法是稳定排序法。

3、C++代码 

#include<iostream>
using namespace std;

void Print(int* array, int size) {
	for (int i = 0; i < size; i++)
		cout << array[i] << "  ";
	cout << endl;
}

void Merge(int* array, int left, int mid, int right) {
	int* tempArray = new int[right - left + 1];
	int k = 0;
	int left_1 = left;
	int left_2 = mid + 1;

	while (left_1 <= mid && left_2 <= right) {
		if (array[left_1] <= array[left_2])
			tempArray[k++] = array[left_1++];
		else
			tempArray[k++] = array[left_2++];
	}

	while (left_1 <= mid)
		tempArray[k++] = array[left_1++];

	while (left_2 <= right)
		tempArray[k++] = array[left_2++];

	for (int i = left, j = 0; i <= right; i++, j++)
		array[i] = tempArray[j];

	tempArray = nullptr;
	delete tempArray;
}

void MergeSort(int* array, int leftIndex, int rightIndex) {
	if (leftIndex == rightIndex)
		return;

	int midIndex = (leftIndex + rightIndex) / 2;
	//分治
	MergeSort(array, leftIndex, midIndex);
	MergeSort(array, midIndex + 1, rightIndex);
	//合并
	Merge(array, leftIndex, midIndex, rightIndex);
}

int main() {
	int data[10] = { 32,5,24,55,40,81,17,48,25,71 };
	cout << "原始数据：" << endl;
	Print(data, 10);
	MergeSort(data, 0, 9);
	//5  32  24  55  40  81  17  48  25  71
	//5  24  32  55  40  81  17  48  25  71
	//5  24  32  40  55  81  17  48  25  71
	//5  24  32  40  55  81  17  48  25  71
	//5  24  32  40  55  17  81  48  25  71
	//5  24  32  40  55  17  48  81  25  71
	//5  24  32  40  55  17  48  81  25  71
	//5  24  32  40  55  17  25  48  71  81
	//5  17  24  25  32  40  48  55  71  81
	cout << "最终数据：" << endl;
	Print(data, 10);
	return 0;
}

输出结果