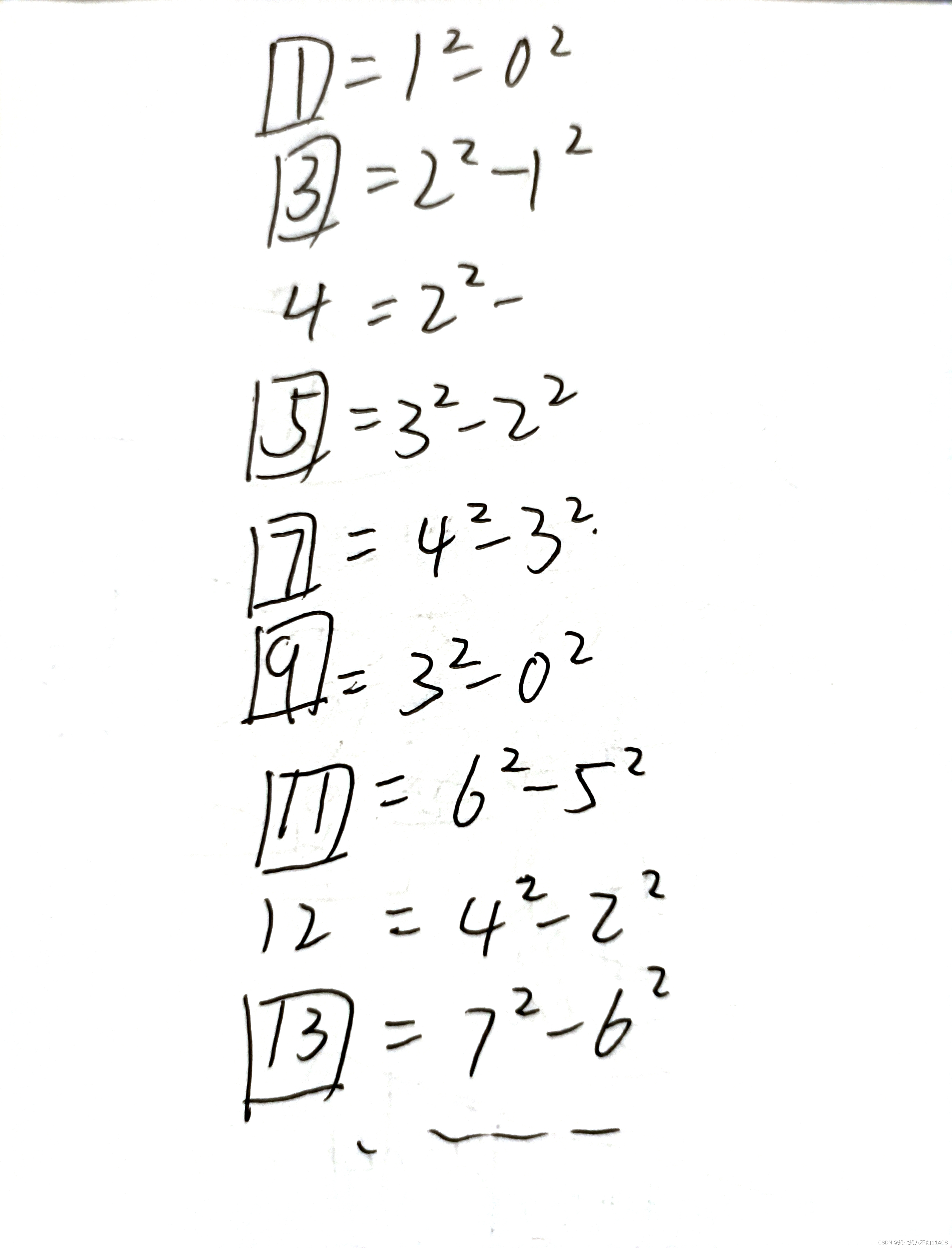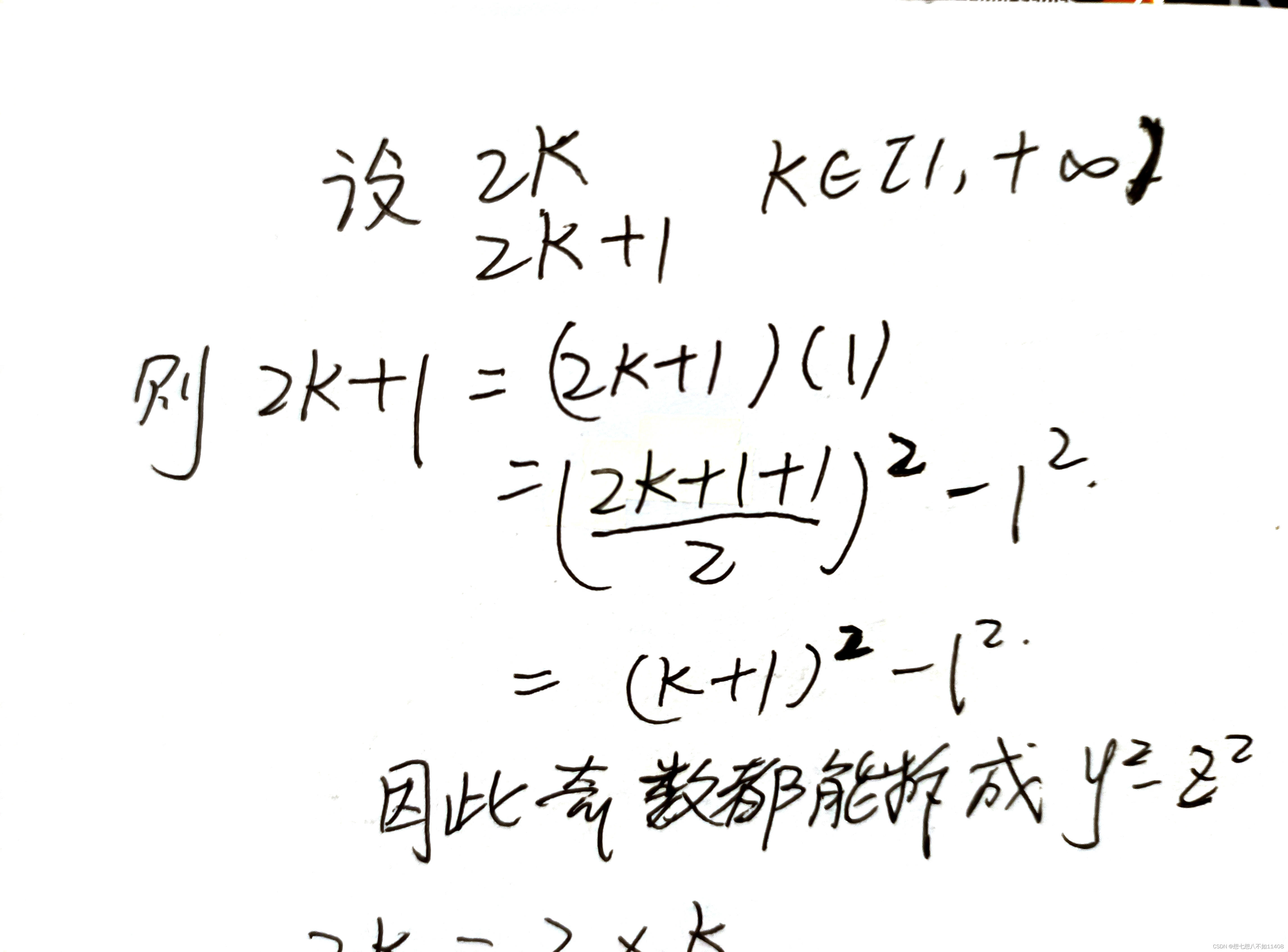蓝桥杯2023年第十四届省赛真题-平方差 - C语言网 (dotcpp.com)

 初步想法，x = y2 − z2=（y+z)(y-z)

即x=a*b，a=y+z，b=y-z

2y=a+b

即a+b是2的倍数就好了。

即x存在两个因数之和为偶数就能满足条件。

但时间是（r-l）*x，数据1e9，直接T了

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
map<int,int> mp;
int cnt;

bool judge(int  x)
{
	for(int i=1;i<=x;i++)//找两个因数 
	{
		if(x%i!=0) continue;
		int d=x/i+i;
		if(d%2==0||x==1)//说明是整数 
		{
			return true; 
		} 
	}
	return false;
}
signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	
	int l,r;
	cin>>l>>r; 
	
	for(int i=l;i<=r;i++)
	{
		if(judge(i)) cnt++; 
	}
	cout<<cnt;
    return 0;
}

运行结果：

进一步分析：

根据题意多写几个，不难发现奇数似乎都能拆成y2 − z2的形式？因此，我们从奇偶的角度来找规律。

(这个地方写错了，是

那么，在这里就可以得出结论辣。想要数字能表示成y2-z2的形式，只有两种可能：

1.奇数   2.4的倍数

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int cnt;

signed main()
{
	int l,r;
	cin>>l>>r; 
	
	for(int i=l;i<=r;i++)
	{
		if(i%2) cnt++;
		if(i%4==0) cnt++;
	}
	cout<<cnt;
    return 0;
}

 （这一步还不能过属实有点钻牛角尖了。。。。。

但是好在，已知一个数x，对应的奇数、4的倍数的数的个数是可以算出来的。

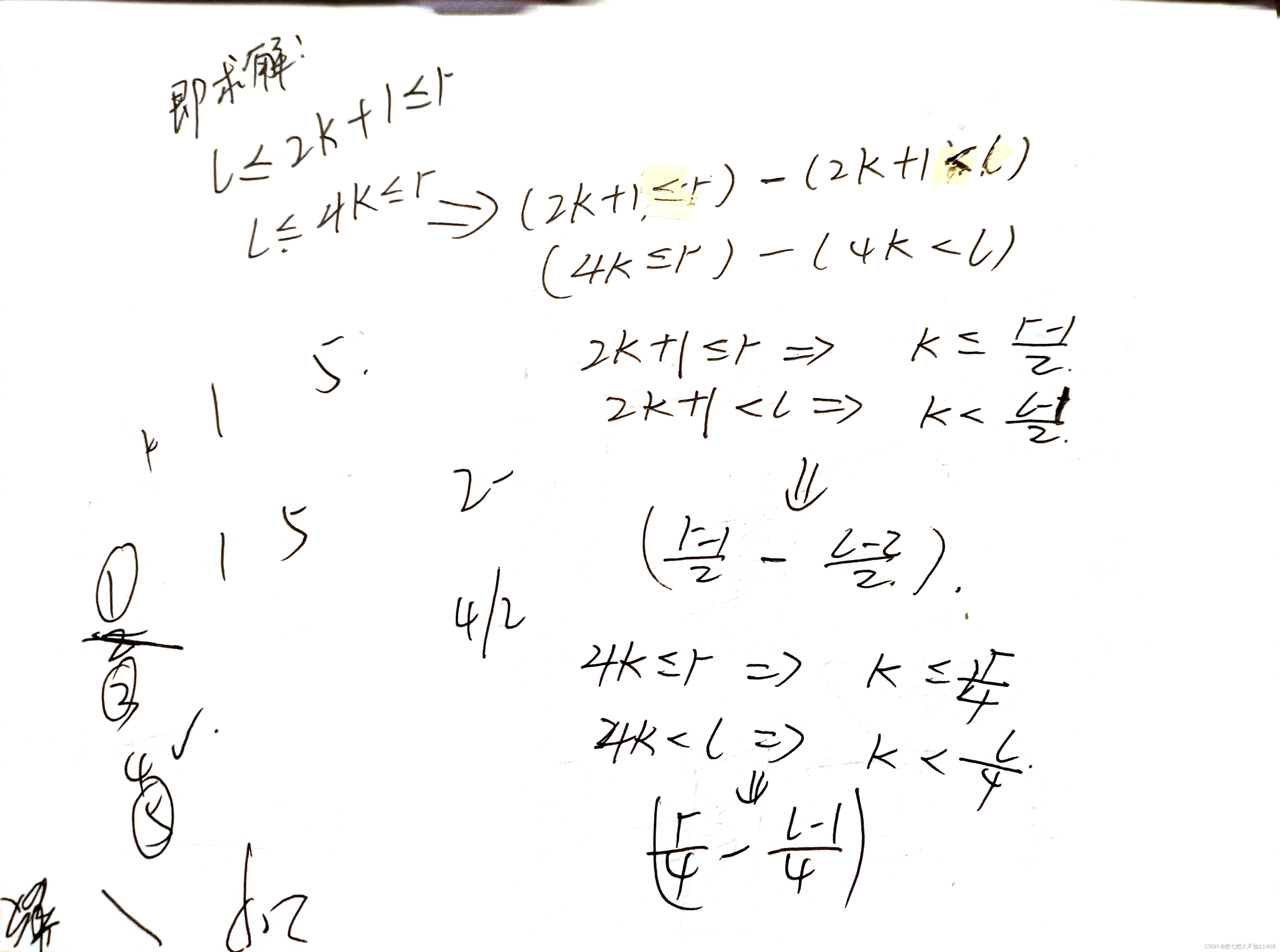
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int cnt;
signed main()
{
	int l,r;
	cin>>l>>r; 
	
	int d=(l-1)/2;
	if((l-1)%2==0) d--;
	
	int p=l/4;
	if((l%4)==0) p--;
	
	cnt=(r-1)/2-d+r/4-p;
	cout<<cnt;
    return 0;
}