毫米波雷达系列 | 传统CFAR检测（均值类）

CFAR检测器主要用于检测背景杂波环境中的雷达目标，常见的均值类CFAR检测器包括单元平均检测器(CA-CFAR)、选择最大检测器(GO-CFAR)、选择最小检测器(SO-CFAR)。

CFAR检测器的性能取决于窗口的大小和形状，以及阈值的设置。通常，选择合适的窗口和阈值需要进行大量的实验和测试，以便在各种条件下获得最佳性能。

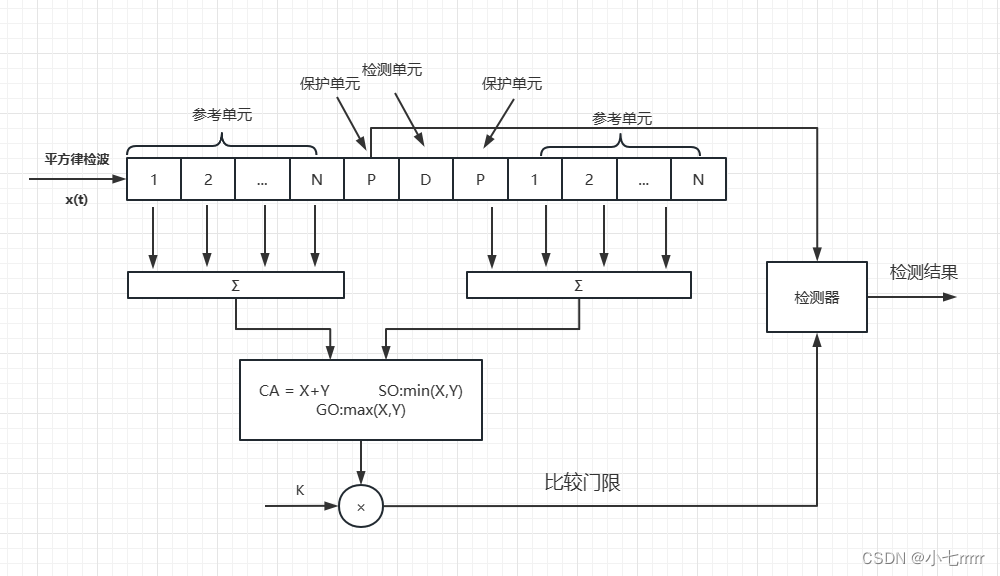
CFAR检测器将窗口分为三类：参考单元、保护单元和检测单元。

其中参考单元用来估算背景杂波功率值，保护单元用来防止检测单元的能量泄漏到参考单元。

1.CA-CFAR算法

CA-CFAR 是指，在待检测单元两侧各取 N 个参考单元，计算总共2N 个参考单元的平均值，当作背景杂波功率估计值 Z_ca。所以待检测单元 D 两侧参考单元计算表达式为:

Z c a = ( X + Y ) / 2 = 1 2 N （ ∑ i = 1 N x i + ∑ i = 1 N y i ） Zca = (X+Y)/2=frac{1}{2N}（sum_{i=1}^{N}{x_i}+sum_{i=1}^{N}{y_i}） Zca=(X+Y)/2=2N1​（i=1∑N​xi​+i=1∑N​yi​）
将背景杂波功率估计值 Z_ca乘以门限乘积因子k，就得到待检测单元D的门限值S。
S = k Z c a = k 2 N （ ∑ i = 1 N x i + ∑ i = 1 N y i ） S=kZca=frac{k}{2N}（sum_{i=1}^{N}{x_i}+sum_{i=1}^{N}{y_i}） S=kZca=2Nk​（i=1∑N​xi​+i=1∑N​yi​）

2.SO-CFRA算法

SO-CFAR 是指，对参考单元分别计算其平均值 X 和Y，并选取X 和Y中平均值较小的当作待检测单元D的背景杂波功率估计值 Zso。
$$Zso=min(X,Y)$$

X = ∑ i = 1 N x i X=sum_{i=1}^{N}{x_i} X=i=1∑N​xi​

Y = ∑ i = 1 N y i Y=sum_{i=1}^{N}{y_i} Y=i=1∑N​yi​

检测门限S可以表示为:
$$S=kZso$$

3.GO-CFAR算法

GO-CFAR 是指，对参考单元分别计算其平均值 X 和Y，并选取 X 和Y中平均值较大的当作待检测单元 D 的背景杂波功率估计值 Z_GO。
$$Zgo=max(X,Y)$$
检测门限S可以表示为:
$$S=kZgo$$

4.仿真对比

在均匀杂波环境、多目标环境和杂波边缘环境中对均值类CFAR检测器的性能进行比较分析。

参数设置：

虚警概率	10-4
参考单元	32
保护单元	4
信噪比SNR	20
多目标单元位置	110和120
杂波边缘功率	20dB、30dB

1）均匀背景

2）多目标

3）杂波边缘环境

三种均值类检测器在均匀环境中都可以在第110个距离单元检测出目标，三种检测器的性能基本无差异；

在多目标环境中，可以看到只有SO-CFAR成功将两个目标检测到，而CA-CFAR和GO-CFAR对第110个距离单元的目标漏检。第120个距离单元的目标为信噪比较强的信号，在运算的过程中加入到了参考单元中，使得整个背景杂波功率估计值变高，因此检测门限提高，从而导致了漏检。SO-CFAR检测器采取的策略是选择小的背景功率估计值，所以可以将两个目标都检测到；

在杂波边缘环境中，在第100个距离单位处的目标只有GO-CFAR算法检测成功，CA-CFAR和SO-CFAR均出现了漏检现象，说明GO-CFAR在杂波边缘环境下的虚警能力控制更强

clc;
close all;
clear all;
%% 均匀背景噪声（单目标&多目标）
clear
close all;
shape=200;
variance=200;
noise_db=20;
noise_p=10.^(noise_db./10);%噪声的实际功率
show_out=0;
[ xc ] = env_uniform(variance,  shape, noise_db,show_out);% 产生信号

% 多目标
locatsite=[80,110,120];
% SNR1=12;signal1_p=10.^(SNR1./10).*noise_p(1,end);
SNR2=15;signal2_p=10.^(SNR2./10).*noise_p(1,end);
SNR3=18;signal3_p=10.^(SNR3./10).*noise_p(1,end);
% xc(1,locatsite(1))=signal1_p;
xc(1,locatsite(2))=signal2_p;
xc(1,locatsite())=signal3_p;
trgt = zeros(length(locatsite),2);
% trgt(1,:) = [locatsite(1),signal1_p];
trgt(2,:) = [locatsite(2),signal2_p];
trgt(3,:) = [locatsite(3),signal3_p];
%% 算法结果&图谱显示
N=32;
pro_N=4;
PAD=10^(-4); % 虚警概率

% xc为信号；pro_N为保护单元；PAD为虚警概率
% XT为CFAR的检测门限
[ XT_CA ] = cfar_ac( abs(xc), N, pro_N, PAD);%计算CACFAR
[ XT_GO ] = cfar_go( abs(xc), N, pro_N, PAD);%计算CACFAR
[ XT_SO ] = cfar_so( abs(xc), N, pro_N, PAD);%计算CACFAR

plotNum=20;
markersize=5;
LineWidth=1.25;
len=length(xc);
figure;
plot(10.*log(abs(xc))./log(10),'LineWidth',LineWidth),hold on;
plot(10.*log(abs(XT_CA))./log(10),'g-+','MarkerIndices',1:plotNum:len),hold on;
plot(10.*log(abs(XT_GO))./log(10),'r-*','MarkerIndices',30:plotNum:len),hold on;
plot(10.*log(abs(XT_SO))./log(10),'b-^','MarkerIndices',60:plotNum:len),hold on;
trgtFlag = exist('trgt','var') ;
if trgtFlag%有无目标点
    plot(trgt(:,1),10.*log(abs(trgt(:,2)))./log(10),'s','Color',[1 0 1],'MarkerSize',markersize),hold on;
end
title('CA-GO-SO-CFAR处理效果图');
xlabel('频谱单元');ylabel('幅度/dB');
legend('信号','CA-CFAR','GO-CFAR','SO-CFAR','目标点','Location','SouthEast');

% 均匀背景
function [ xc ] = env_uniform(variance,  shape, power_db, show_out)
if (nargin==3)
    show_out=0;
end
c=10^(power_db/10);     % 这里是幅度——功率，实际的噪声功率
xc=c + random('Normal',0,variance,1,shape);%产生一个正态分布/高斯分布的噪声，期望为0，标准差为200，1*200的矩阵
if show_out==1
    figure;plot(10.*log(abs(xc))./log(10));
end
end

% 杂波背景
function [ xc ] = env_edge(variance,  shape, power_db, show_out)
if (nargin==3)
    show_out=0;
end
c=10.^(power_db./10);               % 这里是幅度——功率
xc=random('Normal',0,variance,1,shape(1,end)); % 正常分布 期望为0 方差为200 1*2矩阵
xc(1,1:end)=xc(1,1:end)+c(1,1);% 前面20
index=1;
for i=1:length(power_db)
    xc(1,index:shape(1,i))=xc(1,index:shape(1,i)).*c(1,i)./c(1,1);
    index=shape(1,i)+1;
end
if show_out==1
    figure;plot(20.*log(abs(xc))./log(10));
end
end