数据结构——栈(C语言版)

一、栈的性质

1.栈是一种特殊的线性结构，与线性表不同的是栈只能在一端进行操作，另一端是锁死的，是操作受限的线性表
2.栈限定只能在栈顶进行数据的插入和删除
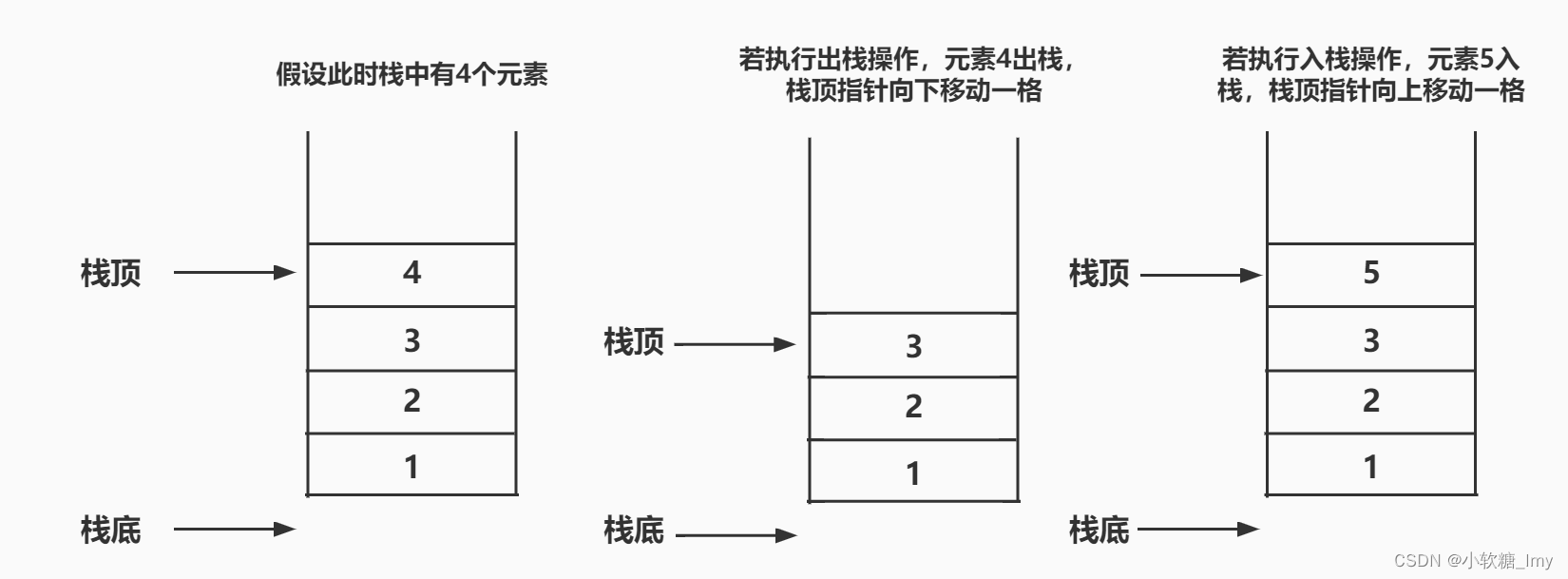
3.栈中的数据元素遵循先进后出的原则（FILO），最先进栈的元素在最底部，最后进栈的元素在栈的顶部（类似于往空箱子放物品，最先放的物品在最底部，最后放的物体在最上面，能最先被取出）

二、栈的常用操作

1.初始化栈
2.压栈，往栈中添加一个元素
3.弹栈，从栈顶删除一个元素
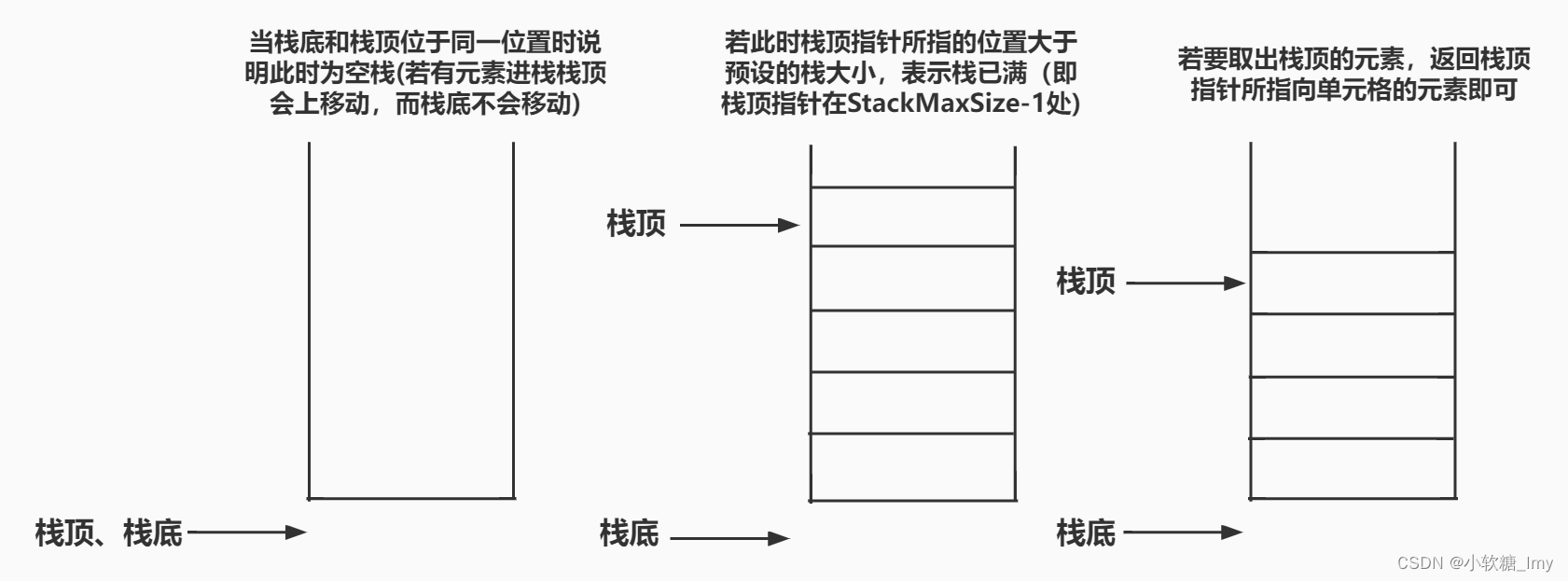
4.获取栈顶元素
5.判断栈是否为空、是否满栈
注意：在操作栈时，要避免“上溢”和“下溢”
上溢：指栈已满，若继续存数据，则会上溢，出现报错（栈满再存出现上溢）
下溢：指栈已空，若继续取数据，则会下溢，出现报错（栈空再取出现下溢）
下面以线性栈为基础，下面用图解详细说明各个操作的过程
（本文栈底设定为-1，与课本有所不同，但更易理解）

元素出栈和进栈(注意栈顶的变化)

注意：若栈满时，无法执行入栈操作，当栈空时，无法出栈及获取栈顶元素

1.定义栈的结构体(以int为例）

typedef struct
{
	int stack[MaxStackSize]; //可以根据不同的数据类型进行更换，MaxStackSize定义了栈大小
	int top; //定义此时栈顶元素的位置(数组下标)，每次入栈pos会自增1,再把相应的元素入栈
}SequenceStack;

2.栈的初始化

void StackInit(SequenceStack *S)
{
	S->top = -1; //让栈顶指针移动至-1位(最底)
}

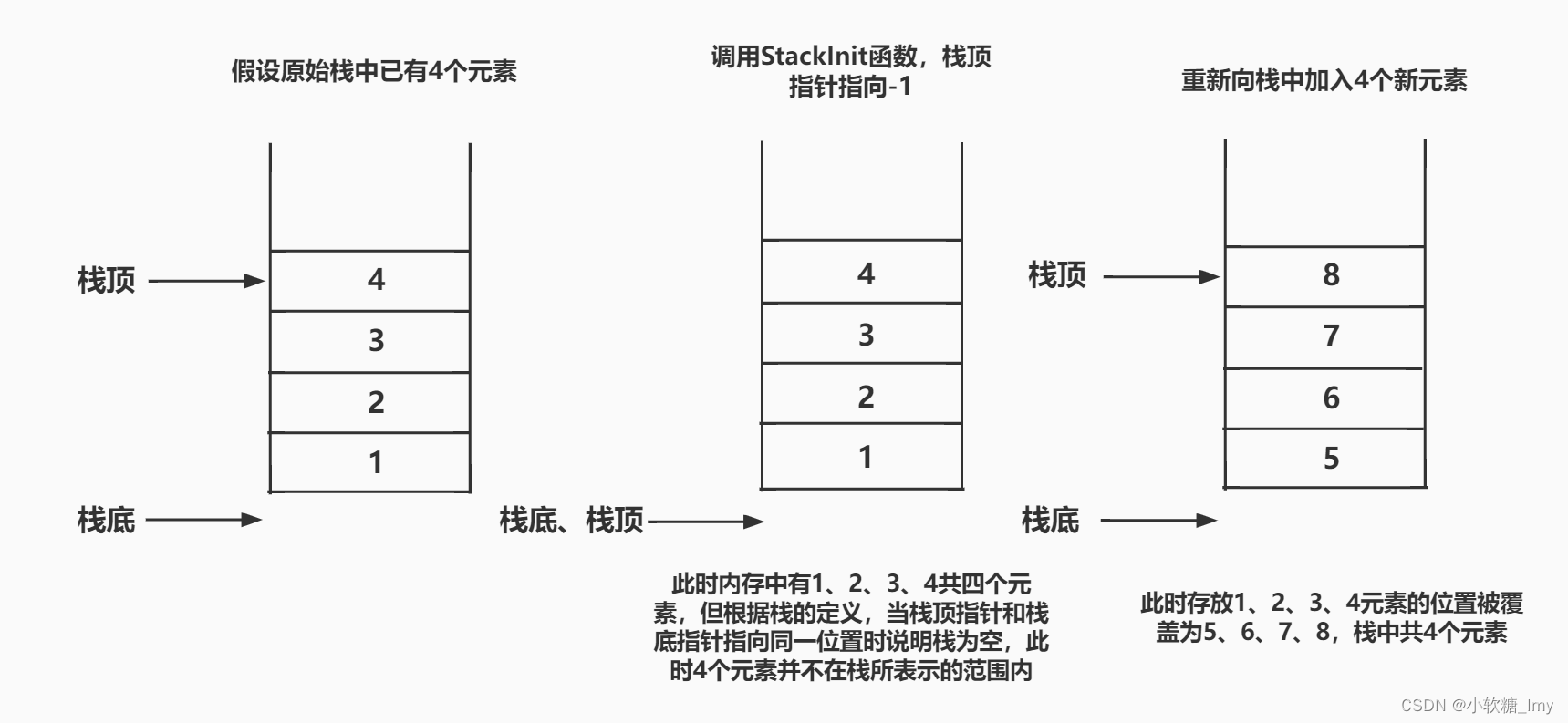
可能会有疑问，假设此时栈里已经有几个元素了，仅用S->top = -1就可以使栈初始化吗？
S->top = -1就可以使栈初始化。注意：栈的范围是栈顶到栈底，下面用图来解释

3.判断此时栈是否为空

bool JudgeStackEmpty(SequenceStack *S) //为空返回true，非空返回false
{
	if(S->top == -1)  // 判断此时栈顶指针是否和栈底指针是否重合(栈底默认为-1)
		return true;
	else
		return false;
}

4.进栈操作

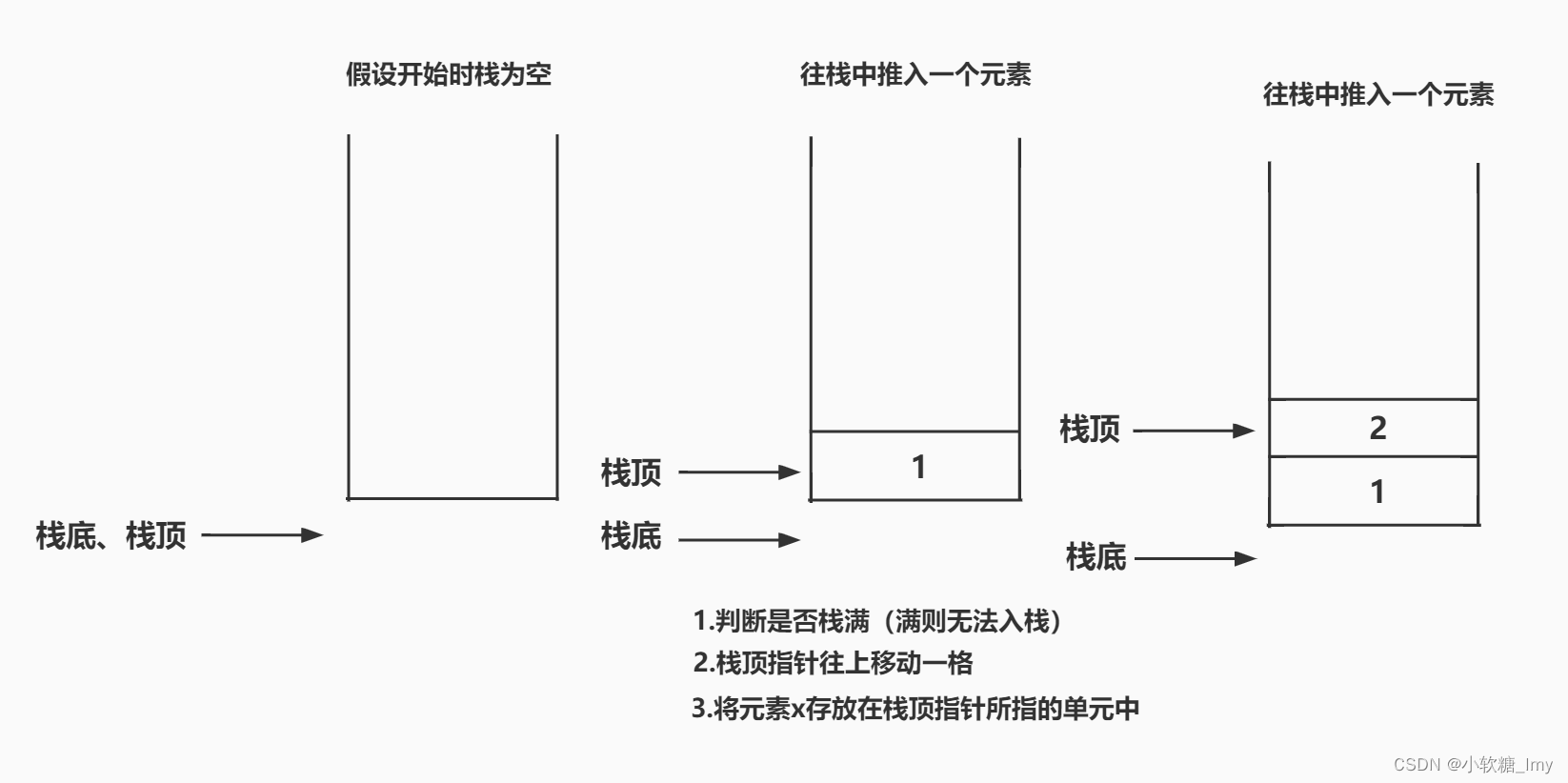
进栈操作需要考虑到栈的大小问题，若此时栈已满，无法将元素进栈，若继续进栈会出现上溢问题。因此进栈操作前需判断栈的大小问题，若未满，可以进栈；栈已满，不能进栈。

void StackPush(SequenceStack *S,int x)
{
	if(S->top == MaxStackSize - 1){  
		printf("此时栈满");  //若栈满继续入栈会出现上溢问题
	}
	else{
		S->top++;  //栈顶指针往上移动一格
		S->stack[S->top] = x;   //将元素x存放在栈顶指针所指单元中
		printf("入栈成功");
	}
}

进栈的过程由下图解释

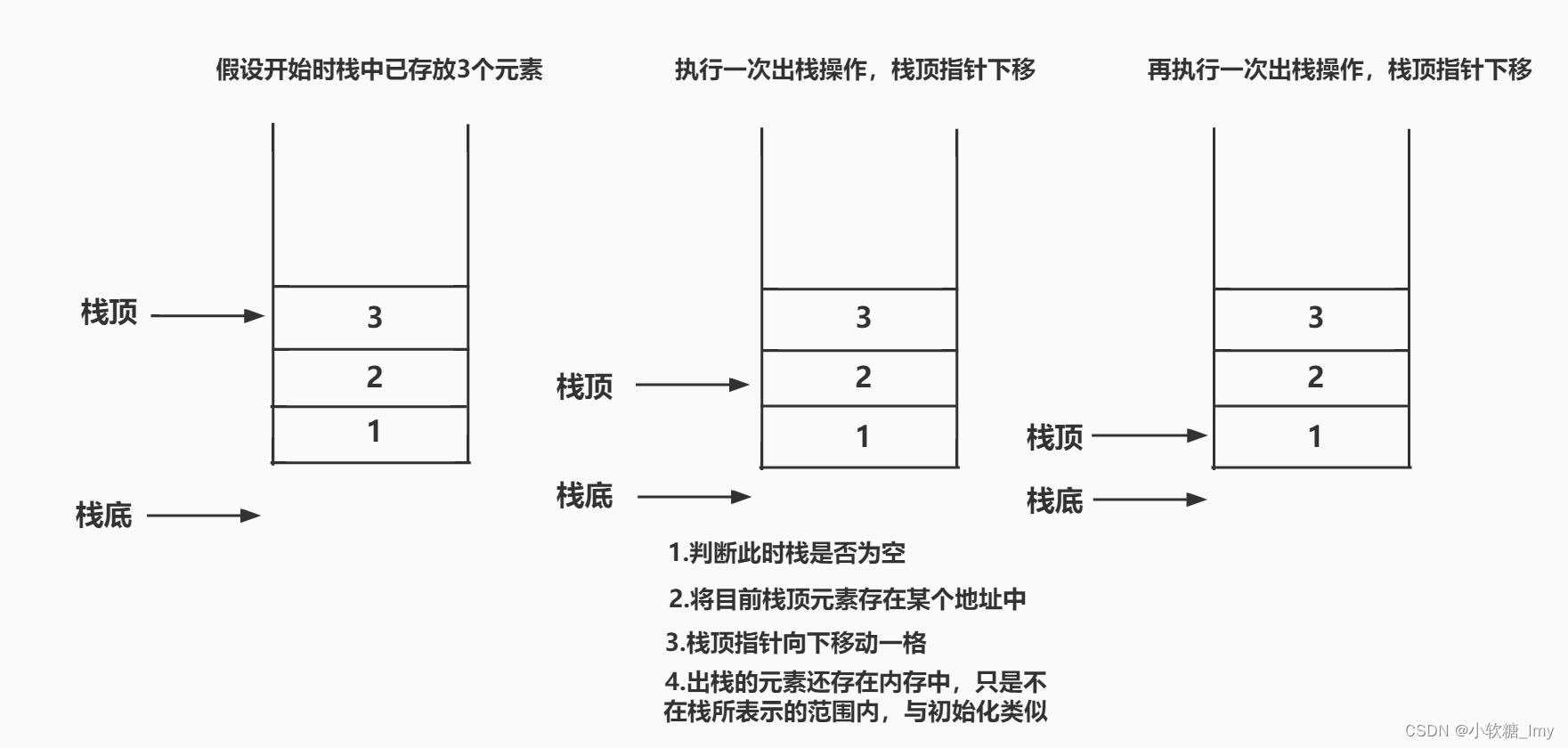
5.出栈操作（删除栈顶元素，用变量x返回）

出栈操作需要考虑到栈的大小问题，若此时栈已空，无法将元素出栈，若继续出栈会出现下溢问题。因此出栈操作前需判断栈是否为空的问题，若非空，可以出栈；栈空，则不能出栈。

int StackPop(SequenceStack *S)
{
	if(S->top == -1){
		printf("此时为空栈，无法继续出栈"); //若栈空仍继续出栈，会出现下溢问题
		return -1;//-1表示出栈失败
	}
	int x = S->stack[S->top]; 
	S->top--; //栈顶指针下移，表示出栈了一个元素
	return x;
}

出栈的过程由下图解释

6.取栈顶元素

int GetStackTop(SequenceStack *S)
{
	if(S->top == -1)  //判断此时是否为空
		return -1; //-1表示此时无法取栈顶元素（可以根据题目要求进行调整)
	int x = S->stack[S->top]; //类似于出栈存x的操作，但无需动栈顶指针
	return x;
}

三、栈的习题

题源：leetcode剑指Offer 27 回文链表
网址：https://leetcode.cn/problems/aMhZSa/
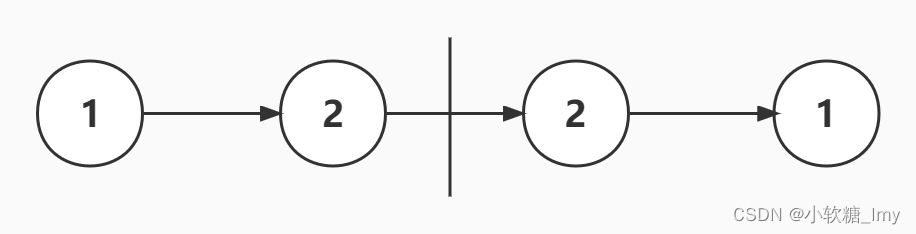
思路：要判断该链表是否为回文的，根据回文的特性，只需要看正序遍历一次以及反序遍历一次的结果是否相等即可判断是否为回文串，利用栈的先进后出的特性，恰好能做到反序遍历该链表，每次只需对比正序遍历的元素与此时栈顶元素是否相等。若相等，则出栈，对比下一个元素；若不相等，表示不是回文链表。

如上图所示，正序遍历的结果是1-2-2-1，反序遍历的结果是1-2-2-1，相同证明是回文链表。
代码如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
#define MaxStackSize 100001
int a[100001];
typedef struct
{
	int stack[MaxStackSize]; 
	int top; 
}SequenceStack;
void StackInit(SequenceStack *S)
{
	S->top = -1;
}
void StackPush(SequenceStack *S,int x)
{
	if(S->top == MaxStackSize - 1)
		printf("此时栈满"); 
	else{
		S->top++; 
		S->stack[S->top] = x;   
	}
}
int StackPop(SequenceStack *S)
{
	if(S->top == -1){
		return -1;
	}
	int x = S->stack[S->top]; 
	S->top--;
	return x;
}
int GetStackTop(SequenceStack *S)
{
	if(S->top == -1)  
		return -1;
	int x = S->stack[S->top];
	return x;
}
bool JudgeStackEmpty(SequenceStack *S)
{
	if(S->top == -1)
		return true;
	else
		return false;
}
bool isPalindrome(struct ListNode* head){
    int i = 0;
    SequenceStack myStack;
    StackInit(&myStack);  //首先初始化栈
    while(head != NULL){
        StackPush(&myStack,head->val); //把链表当前指针所指的元素入栈
        a[i] = head->val; //用数组记录正序遍历链表元素的过程
        i++; 
        head = head->next; //头指针指向下一个元素处
    }
    int now = 0;
    while(!JudgeStackEmpty(&myStack)){
        int t = GetStackTop(&myStack); //取出栈顶的元素，代表后序遍历的结果
        StackPop(&myStack);  //将栈顶元素弹出
        if(t != a[now])  //若正序遍历链表的值与反序遍历的值不相同，代表不是回文链表
            return false;
        now++; //元素出栈后now指针也需要往后移动一位，对比下一组
    }
    return true;
}

改良版做法：由于回文链表存在中间对称的特性，因此可以只将前半部分入栈，将前半部分进栈，相当于后序遍历，后半部分进行正序遍历，判断条件和上述代码完全一样

推荐尝试关于栈的题目：
1.有效的括号https://leetcode.cn/problems/valid-parentheses/
2.验证栈序列https://leetcode.cn/problems/validate-stack-sequences/
如果条件允许，建议大家去了解一下c++的STL模板库，实现栈的各种功能更简便