计算复杂度

提示：计算复杂度的简单理解(第一次写博客)

计算复杂度

计算复杂度

计算复杂度

我们以Vicinity Vision Transformer论文中的图为例。
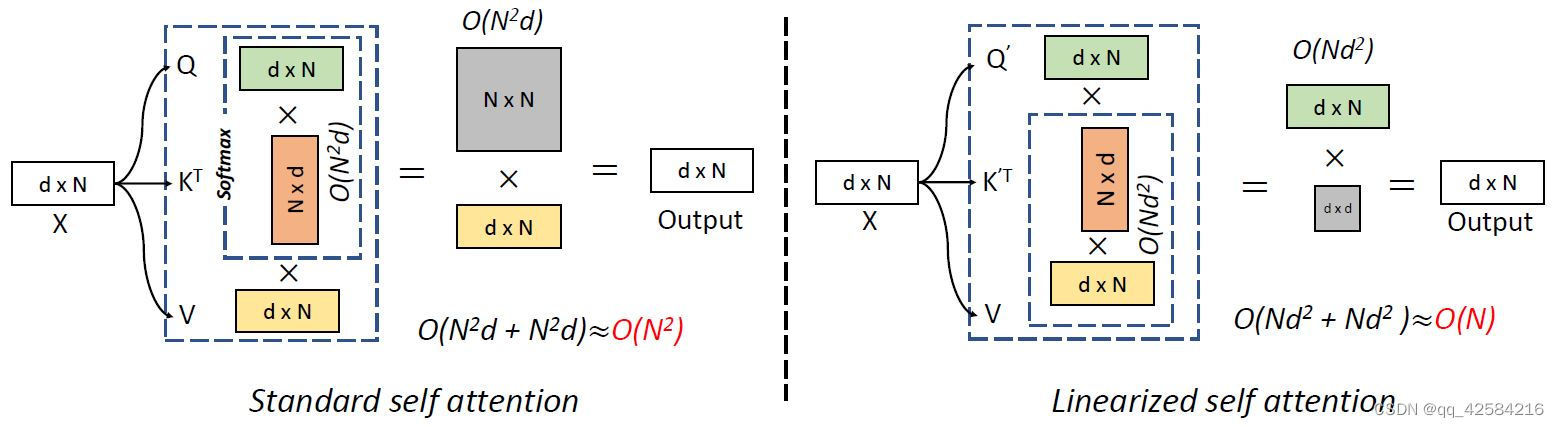在这里插入图片描述图注：标准自注意力(左)和线性化自注意力(右)的图示。 $N$ 表示输入图像的 $p a t c h$ 数， $d$ 是特征维度。使 $N ≫ d$ ，线性化自注意力的计算复杂度相对于输入长度线性增长，而标准自注意力的计算复杂度是二次的。

从输入到输出可以这样计算：
$(N \times d) \times (d \times N) = N \times N \times (d \times N) \times (N \times N) = d \times N$
$(d \times N) \times (N \times d) = d \times d \times (d \times d) \times (d \times N) = d \times N$

关于计算复杂度：其实可以认为是乘法次数。我们给出最直观的解释。

假设有两个矩阵做乘法，如下：
$left[begin{matrix}1&2\3&4\5&6\end{matrix}right]timesleft[begin{matrix}1&2&3\4&5&6\end{matrix}right]=left[begin{matrix}1&2&3\4&5&6\7&8&9\end{matrix}right]$ ，其中行数为 $N$ ，列数为 $d$ 。

$(3 \times 2) \times (2 \times 3) = (3 \times 3) \times (N \times d) \times (d \times N) = (N \times N)$

$3 \times 3$ 矩阵第一个元素涉及的乘法次数： $1 \times 1 + 2 \times 4 = 9$ 共2次乘法；其它元素是一样的。最后可以得到 $N=N^{2}d$ .

假设又有两个矩阵做乘法，如下：
$left[begin{matrix}1&2&3\4&5&6\end{matrix}right]timesleft[begin{matrix}1&2\3&4\5&6\end{matrix}right]=left[begin{matrix}1&2\3&4\end{matrix}right]$ ，其中行数为 $d$ ，列数为 $N$ 。

$(2 \times 3) \times (3 \times 2) = (2 \times 2) \times (d \times N) \times (N \times d) = (d \times d)$

$2 \times 2$ 矩阵第一个元素涉及的乘法次数： $1 \times 1 + 2 \times 3 + 2 \times 5 = 17$ 共3次乘法；其它元素是一样的。最后可以得到 $d=Nd^2$ .

为什么会有这种情况呢？以第二个例子为例，可以观察到，所得结果的一个元素的乘法数量和消失的维度大小有关，也就是列数 $N$ ，或者说，列数 $N$ 就是所得结果一个元素的乘法次数。那么多少个元素呢？元素个数就要看你是如何进行的乘法操作，其实就是矩阵大小。比如 $(2 \times 3) \times (3 \times 2) = (2 \times 2) \times (d \times N) \times (N \times d) = (d \times d)$ ，那么就是 $d^2$ 个元素，最后乘法次数就是 $Nd^2$ 。

乘法次数=消失的维度 × 所得矩阵大小。

那么计算复杂度呢？我们不要去管 $O (∙)$ 具体代表什么，这不重要。
以第一个图为例，乘法次数1： $N)=N^{2}d$ ；乘法次数 $2$ ： $N)=N^{2}d$ 。 $O(N^{2}d+N^{2}d)=O(N^2)$ 。因为 $N ≫ d$ ，所以 $d$ (还有常数 $2$ )被省略了，即 $O(N^2)$ 。
以第二个图为例，乘法次数1： $d)=Nd^2$ ；乘法次数2： $N)=Nd^2$ 。 $O(Nd^2+Nd^2)=O(N)$ 。因为 $N ≫ d$ ，所以 $d$ (还有常数2)被省略了，即 $O (N)$ 。

事实告诉我们，我们两个的结果一样，但是我们可以通过控制中间过程减少计算复杂度。