【LeetCode】剑指 Offer <二刷>(4)
目录
题目:剑指 Offer 09. 用两个栈实现队列 - 力扣(LeetCode)
题目:剑指 Offer 10- I. 斐波那契数列 - 力扣(LeetCode)
题目:剑指 Offer 09. 用两个栈实现队列 - 力扣(LeetCode)

题目的接口:
type CQueue struct {
}
func Constructor() CQueue {
}
func (this *CQueue) AppendTail(value int) {
}
func (this *CQueue) DeleteHead() int {
}
/**
* Your CQueue object will be instantiated and called as such:
* obj := Constructor();
* obj.AppendTail(value);
* param_2 := obj.DeleteHead();
*/解题思路:
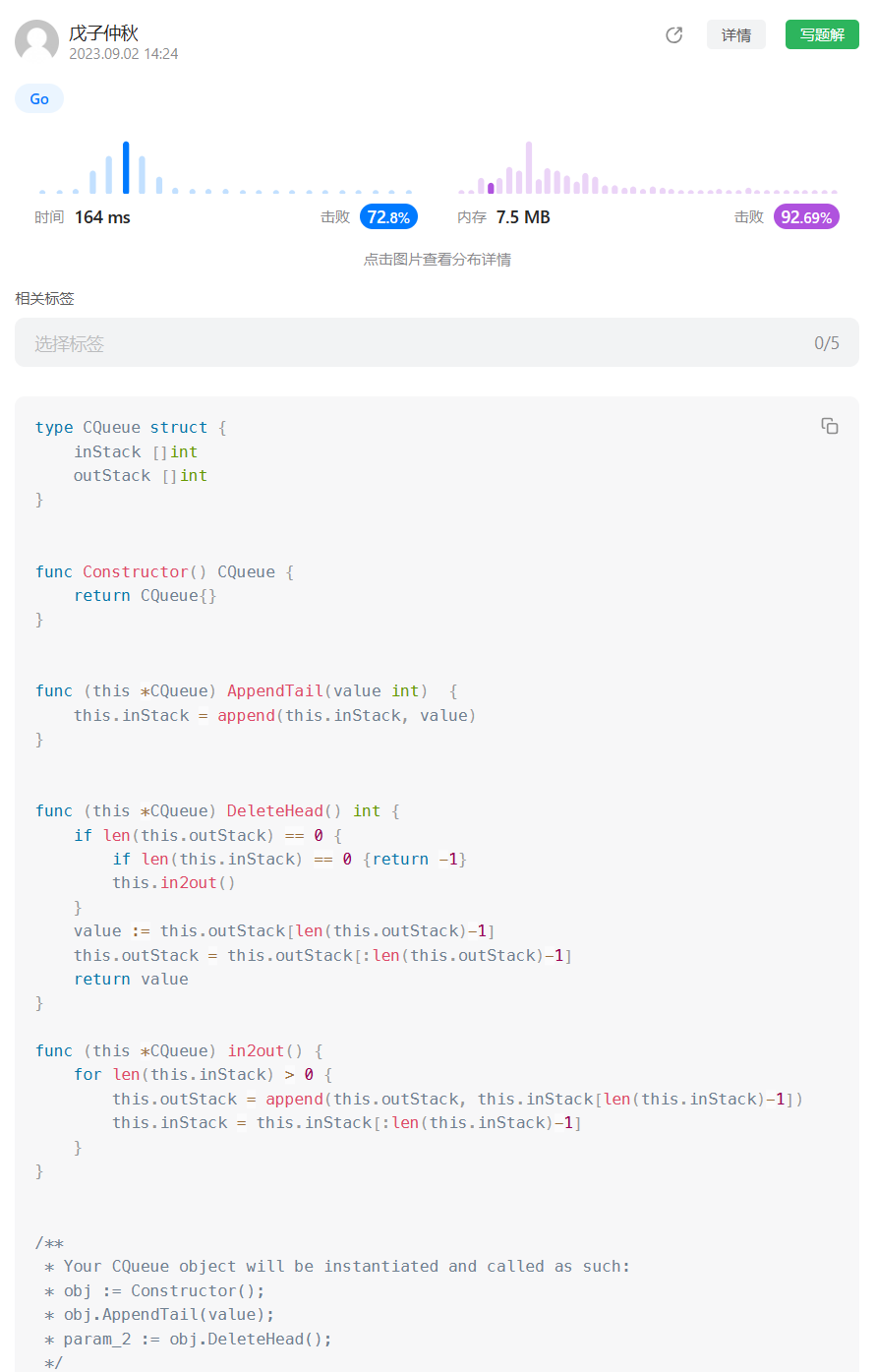
这道题我用 C++ 写的时候是比较简单顺手的,用 STL 可以直接调库调两个栈出来,然后一个作为 inStack,一个作为 OutStack,存入的时候存 inStack,出栈的时候,将 inStack 放进 OutStack 里面,再删除 OutStack 的内容就可以了,
而现在用 golang 来刷这道题,思路不难,主要是怎么样优雅地实现栈结构呢?切片的特性还是很好用的,可以说这下又学会了一个操作,怎么不用下标倒序遍历切片:
this.outStack = append(this.outStack, this.inStack[len(this.inStack)-1])
this.inStack = this.inStack[:len(this.inStack)-1]不断变小 + 不断取最后一个元素就行了,真是妙啊。具体代码如下:
代码:
type CQueue struct {
inStack []int
outStack []int
}
func Constructor() CQueue {
return CQueue{}
}
func (this *CQueue) AppendTail(value int) {
this.inStack = append(this.inStack, value)
}
func (this *CQueue) DeleteHead() int {
if len(this.outStack) == 0 {
if len(this.inStack) == 0 {return -1}
this.in2out()
}
value := this.outStack[len(this.outStack)-1]
this.outStack = this.outStack[:len(this.outStack)-1]
return value
}
func (this *CQueue) in2out() {
for len(this.inStack) > 0 {
this.outStack = append(this.outStack, this.inStack[len(this.inStack)-1])
this.inStack = this.inStack[:len(this.inStack)-1]
}
}
/**
* Your CQueue object will be instantiated and called as such:
* obj := Constructor();
* obj.AppendTail(value);
* param_2 := obj.DeleteHead();
*/过啦!!!
题目:剑指 Offer 10- I. 斐波那契数列 - 力扣(LeetCode)

题目的接口:
func fib(n int) int {
}解题思路:
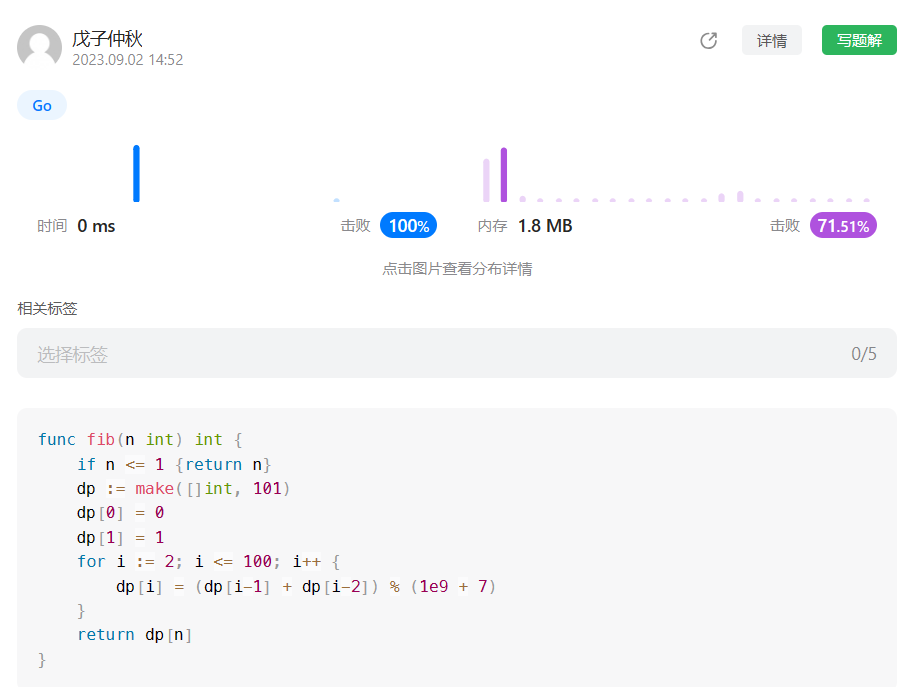
这道题就是非常经典的动态规划入门题目,我这里就直接做了,其实还可以进行空间的优化,但是我觉得没有很大的必要,简单的题没必要,难的题你也优化不出来说实话。
代码:
func fib(n int) int {
if n <= 1 {return n}
dp := make([]int, 101)
dp[0] = 0
dp[1] = 1
for i := 2; i <= 100; i++ {
dp[i] = (dp[i-1] + dp[i-2]) % (1e9 + 7)
}
return dp[n]
}过啦!!!
写在最后:
以上就是本篇文章的内容了,感谢你的阅读。
如果感到有所收获的话可以给博主点一个赞哦。
如果文章内容有遗漏或者错误的地方欢迎私信博主或者在评论区指出~