强化学习—— TD算法(Sarsa算法+Q-learning算法)
强化学习—— TD算法(Sarsa算法+Q-learning算法)
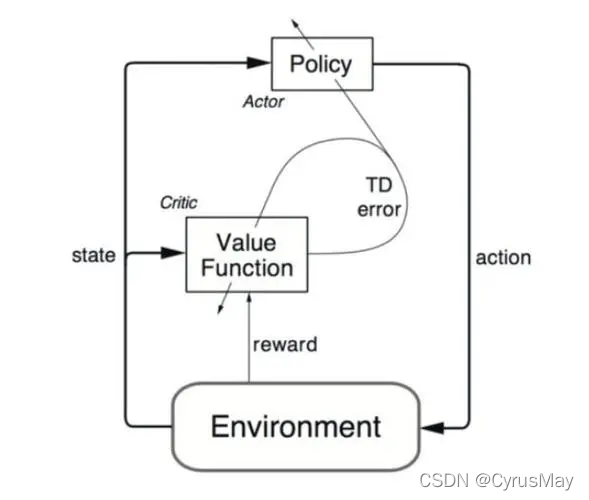
1. Sarsa算法
1.1 TD Target
- 回报函数的定义为:
U t = R t + γ R t + 1 + γ 2 R t + 2 + ⋅ ⋅ ⋅ U t = R t + γ ( R t + 1 + γ R t + 2 + ⋅ ⋅ ⋅ ) U t = R t + γ U t + 1 U_t=R_t+gamma R_{t+1}+gamma^2 R_{t+2}+cdot cdot cdot\ U_t=R_t+gamma (R_{t+1}+gamma R_{t+2}+cdot cdot cdot)\ U_t = R_t+gamma U_{t+1} Ut=Rt+γRt+1+γ2Rt+2+⋅⋅⋅Ut=Rt+γ(Rt+1+γRt+2+⋅⋅⋅)Ut=Rt+γUt+1 - 假设t时刻的回报依赖于t时刻的状态、动作以及t+1时刻的状态: R t ← ( S t , A t , S t + 1 ) R_t gets (S_t,A_t,S_{t+1}) Rt←(St,At,St+1)
- 则动作价值函数可以定义为: Q π ( s t , a t ) = E [ U t ∣ a t , s t ] Q π ( s t , a t ) = E [ R t + γ U t + 1 ∣ a t , s t ] Q π ( s t , a t ) = E [ R t ∣ a t , s t ] + γ E [ U t + 1 ∣ a t , s t ] Q π ( s t , a t ) = E [ R t ∣ a t , s t ] + γ E [ Q π ( S t + 1 , A t + 1 ) ∣ a t , s t ] Q π ( s t , a t ) = E [ R t + γ Q π ( S t + 1 , A t + 1 ) ] Q_pi(s_t,a_t)=E[U_t|a_t,s_t]\ Q_pi(s_t,a_t)=E[R_t+gamma U_{t+1}|a_t,s_t]\Q_pi(s_t,a_t)=E[R_t|a_t,s_t]+gamma E[U_{t+1}|a_t,s_t]\ Q_pi(s_t,a_t)=E[R_t|a_t,s_t]+gamma E[Q_pi(S_{t+1},A_{t+1})|a_t,s_t]\ Q_pi(s_t,a_t) = E[R_t + gamma Q_pi(S_{t+1},A_{t+1})] Qπ(st,at)=E[Ut∣at,st]Qπ(st,at)=E[Rt+γUt+1∣at,st]Qπ(st,at)=E[Rt∣at,st]+γE[Ut+1∣at,st]Qπ(st,at)=E[Rt∣at,st]+γE[Qπ(St+1,At+1)∣at,st]Qπ(st,at)=E[Rt+γQπ(St+1,At+1)]
- 依据蒙特卡洛近似: y t = r t + γ Q π ( s t + 1 , a t + 1 ) y_t= r_t + gamma Q_pi(s_{t+1},a_{t+1}) yt=rt+γQπ(st+1,at+1)
- TD学习的目标: y t ≈ Q π ( s t , a t ) y_t approx Q_pi(s_t,a_t) yt≈Qπ(st,at)
1.2 表格形式的Sarsa算法
- 学习动作价值函数 Q π ( s , a ) Q_pi(s,a) Qπ(s,a)
- 假设动作和状态的数量有限。
- 则需要学习下列表格信息:
| SA | a 1 a_1 a1 | a 2 a_2 a2 | a 3 a_3 a3 | a 4 a_4 a4 | … |
|---|---|---|---|---|---|
| s 1 s_1 s1 | Q 11 Q_{11} Q11 | … | |||
| s 2 s_2 s2 | … | ||||
| s 3 s_3 s3 | … | ||||
| s 4 s_4 s4 | … | ||||
| … | … |
计算步骤为:
- 观测到一个transition,即: ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1)
- 依据策略函函数对动作进行抽样: a t + 1 ∼ π ( ⋅ ∣ s t + 1 ) a_{t+1}sim pi(cdot|s_{t+1}) at+1∼π(⋅∣st+1)
- 查表得到TD Target: y t = r t + γ Q π ( s t + 1 , a t + 1 ) y_t = r_t+gamma Q_pi(s_{t+1},a_{t+1}) yt=rt+γQπ(st+1,at+1)
- TD error为: δ t = Q π ( s t , a t ) − y t delta_t=Q_pi(s_t,a_t)-y_t δt=Qπ(st,at)−yt
- 更新表格: Q π ( s t , a t ) ← Q π ( s t , a t ) − α ⋅ δ t Q_pi(s_t,a_t)gets Q_pi(s_t,a_t) - alpha cdot delta_t Qπ(st,at)←Qπ(st,at)−α⋅δt
1.3 神经网络形式的Sarsa算法
- 用神经网络近似动作价值函数: q ( s , q ; W ) ∼ Q π ( s , a ) q(s,q;W)sim Q_pi(s,a) q(s,q;W)∼Qπ(s,a)
- 神经网络作为裁判去评判动作
- 参数W需要学习
- TD Target为: y t = r t + γ ⋅ q ( s t + 1 , a t + 1 ; W ) y_t = r_t+gamma cdot q(s_{t+1},a_{t+1};W) yt=rt+γ⋅q(st+1,at+1;W)
- TD error为: δ t = q ( s t , a t ; W ) − y t delta_t = q(s_t,a_t;W)-y_t δt=q(st,at;W)−yt
- loss 为: 1 2 ⋅ δ t 2 frac{1}{2}cdot delta_t^2 21⋅δt2
- 梯度为: δ t ⋅ ∂ q ( s t , a t ; W ) ∂ W delta_t cdot frac{partial q(s_t,a_t;W)}{partial W} δt⋅∂W∂q(st,at;W)
- 进行梯度下降: W ← W − α ⋅ δ t ⋅ ∂ q ( s t , a t ; W ) ∂ W Wgets W - alpha cdot delta_t cdot frac{partial q(s_t,a_t;W)}{partial W} W←W−α⋅δt⋅∂W∂q(st,at;W)
2. Q-learning算法
Q-learning用来学习最优动作价值函数: Q π ⋆ ( s , a ) Q_pi^star (s,a) Qπ⋆(s,a)
2.1 TD Target
Q
π
(
s
t
,
a
t
)
=
E
[
R
t
+
γ
⋅
Q
π
(
S
t
+
1
,
A
t
+
1
)
]
Q_pi(s_t,a_t) = E[R_t+gamma cdot Q_pi(S_{t+1},A_{t+1})]
Qπ(st,at)=E[Rt+γ⋅Qπ(St+1,At+1)]
将最优策略函数计为:
π
⋆
pi^star
π⋆
则:
Q
⋆
(
s
t
,
a
t
)
=
Q
π
⋆
(
s
t
,
a
t
)
=
E
[
R
t
+
γ
⋅
Q
π
⋆
(
S
t
+
1
,
A
t
+
1
)
]
Q^star(s_t,a_t)=Q_{pi^star}(s_t,a_t)= E[R_t+gamma cdot Q_{pi^star}(S_{t+1},A_{t+1})]
Q⋆(st,at)=Qπ⋆(st,at)=E[Rt+γ⋅Qπ⋆(St+1,At+1)]
t+1时刻的动作按下式进行计算:
A
t
+
1
=
a
r
g
m
a
x
a
Q
⋆
(
s
t
+
1
,
a
)
A_{t+1}=mathop{argmax}limits_{a} Q^star (s_{t+1},a)
At+1=aargmaxQ⋆(st+1,a)
则最优动作价值函数可作如下近似:
Q
⋆
(
s
t
,
a
t
)
=
E
[
R
t
+
γ
⋅
m
a
x
a
Q
⋆
(
S
t
+
1
,
a
)
]
≈
r
t
+
m
a
x
a
Q
⋆
(
s
t
+
1
,
a
)
Q^star(s_t,a_t)=E[R_t+gamma cdot mathop{max}limits_{a}Q^star(S_{t+1},a)]\ approx r_t+mathop{max}limits_{a}Q^star(s_{t+1},a)
Q⋆(st,at)=E[Rt+γ⋅amaxQ⋆(St+1,a)]≈rt+amaxQ⋆(st+1,a)
2.2 表格形式的Q-learning算法
| SA | a 1 a_1 a1 | a 2 a_2 a2 | a 3 a_3 a3 | a 4 a_4 a4 | … |
|---|---|---|---|---|---|
| s 1 ( 找 出 此 行 最 大 的 Q ) s_1(找出此行最大的Q) s1(找出此行最大的Q) | Q 11 Q_{11} Q11 | … | |||
| s 2 s_2 s2 | … | ||||
| s 3 s_3 s3 | … | ||||
| s 4 s_4 s4 | … | ||||
| … | … |
计算步骤为:
- 观测到一个transition,即: ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1)
- TD Target为: y t = r t + m a x a Q ⋆ ( s t + 1 , a ) y_t=r_t+mathop{max}limits_{a}Q^star(s_{t+1},a) yt=rt+amaxQ⋆(st+1,a)
- TD error为: δ t = Q ⋆ ( s t , a t ) − y t delta_t=Q^star(s_t,a_t)-y_t δt=Q⋆(st,at)−yt
- 更新表格: Q ⋆ ( s t , a t ) ← Q ⋆ ( s t , a t ) − α ⋅ δ t Q^star(s_t,a_t)gets Q^star(s_t,a_t) - alpha cdot delta_t Q⋆(st,at)←Q⋆(st,at)−α⋅δt
2.3 神经网络形式的Q-learning算法(DQN)
- 观测到一个transition,即: ( s t , a t , r t , s t + 1 ) (s_t,a_t,r_t,s_{t+1}) (st,at,rt,st+1)
- TD Target为: y t = r t + m a x a Q ( s t + 1 , a ; W ) y_t=r_t+mathop{max}limits_{a}Q(s_{t+1},a;W) yt=rt+amaxQ(st+1,a;W)
- TD error为: δ t = Q ( s t , a t ; W ) − y t delta_t=Q(s_{t},a_t;W)-y_t δt=Q(st,at;W)−yt
- 参数更新: W ← W − α ⋅ δ t ⋅ ∂ Q ( s t , a t ; W ) ∂ W Wgets W - alpha cdot delta_t cdot frac{partial Q(s_t,a_t;W)}{partial W} W←W−α⋅δt⋅∂W∂Q(st,at;W)
3. Saras和Q-learning的区别
- Sarsa学习动作价值函数: Q π ( s , a ) Q_pi(s,a) Qπ(s,a)
- Actor-Critic中的价值网络为用Sarsa训练的
- Q-learning训练最优动作价值函数: Q ⋆ ( s , a ) Q^star(s,a) Q⋆(s,a)
4. Multi-step TD Target
- one-step仅使用一个reward: r t r_t rt
- multi-step 使用m个reward: r t , r t + 1 , . . . , t t + m − 1 r_t,r_{t+1},...,t_{t+m-1} rt,rt+1,...,tt+m−1
4.1 Sarsa的Multi-step TD Target
y t = ∑ i = 0 m − 1 λ i r t + i + λ m Q π ( s t + m , a t + m ) y_t = sum_{i=0}^{m-1}lambda^i r_{t+i} + lambda^mQ_pi(s_{t+m},a_{t+m}) yt=i=0∑m−1λirt+i+λmQπ(st+m,at+m)
4.2 Q-learning的Multi-step TD Target
y
t
=
∑
i
=
0
m
−
1
λ
i
r
t
+
i
+
λ
m
m
a
x
a
Q
⋆
(
s
t
+
m
,
a
)
y_t = sum_{i=0}^{m-1}lambda^i r_{t+i} + lambda^mmathop{max}limits_{a}Q^star(s_{t+m},a)
yt=i=0∑m−1λirt+i+λmamaxQ⋆(st+m,a)
本文为参考B站学习视频书写的笔记!
by CyrusMay 2022 04 08
我们在小孩和大人的转角
盖一座城堡
——————五月天(好好)——————