1 Introduction

1.1 Machine Learning v.s Statistics

Definition

• Machine Learning : a field that takes an algorithmic approach to data analysis, processing and prediction.

• Algorithmic :produces good predictions or extracts useful information from data to solve a practical problem

Venn diagram: Staticticsdata scienceAI

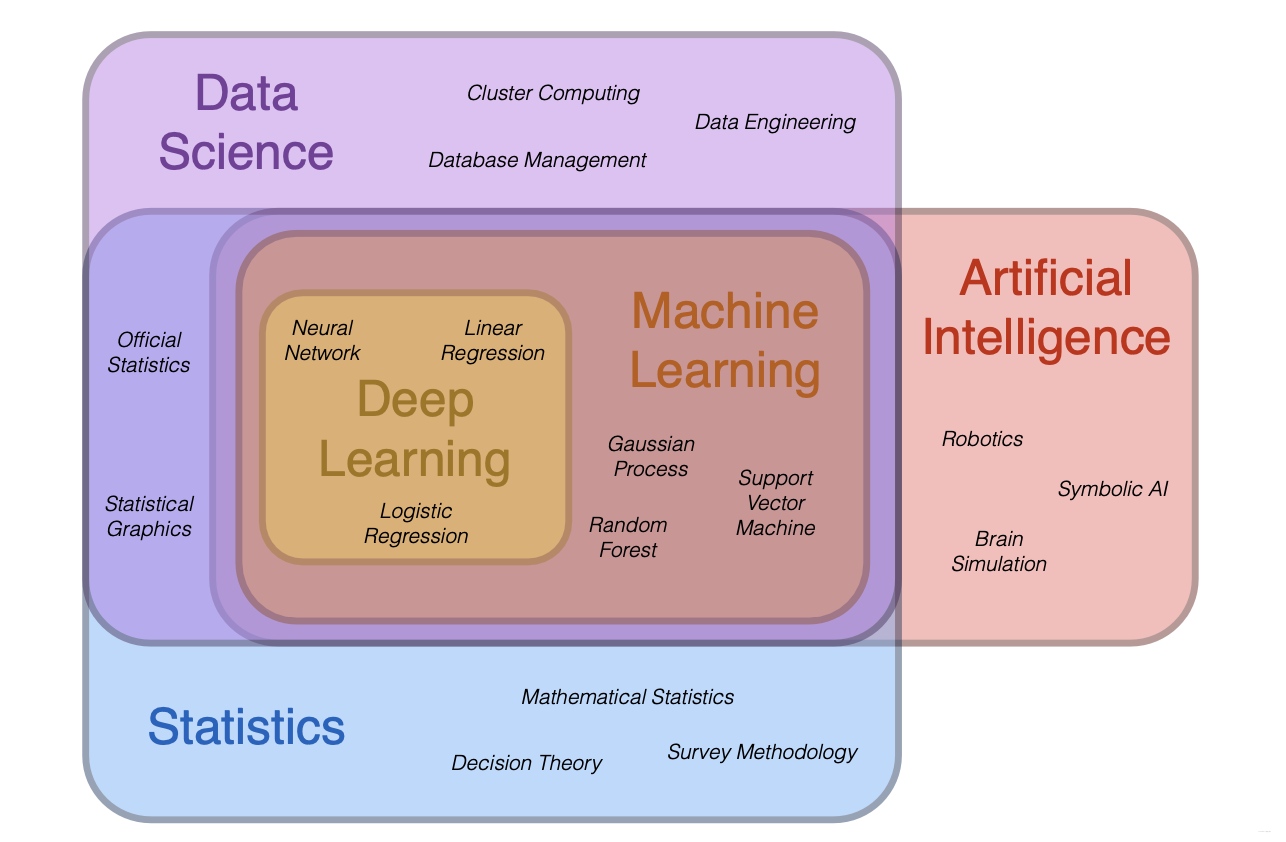
1.2 Applications

Supervised Learning

• Definition:
  Automate decision-making processes by generalising from input-output pairs ( x i , y i ) (x_i , y_i ) (xi​,yi​), $i\in$ {$1,...N$} for some $N\in \mathbb{N}$
• Drawback
  Creating a dataset of inputs and outputs is often a laborious manual process.
• Advantage
  Supervised learning algorithms are well-understood and their performance is easy to measure
• Example(train tickets pricing by distance)

Unsupervised Learning

• Definition
  Only the input data is known, and no known output data is given to the algorithm.
• Drawback
  Harder to understand and evaluate than SL.
• Advantage
  Only the input data is needed and there is no process of “creating input-output pairs” involved.
• Example(trade portfolio)

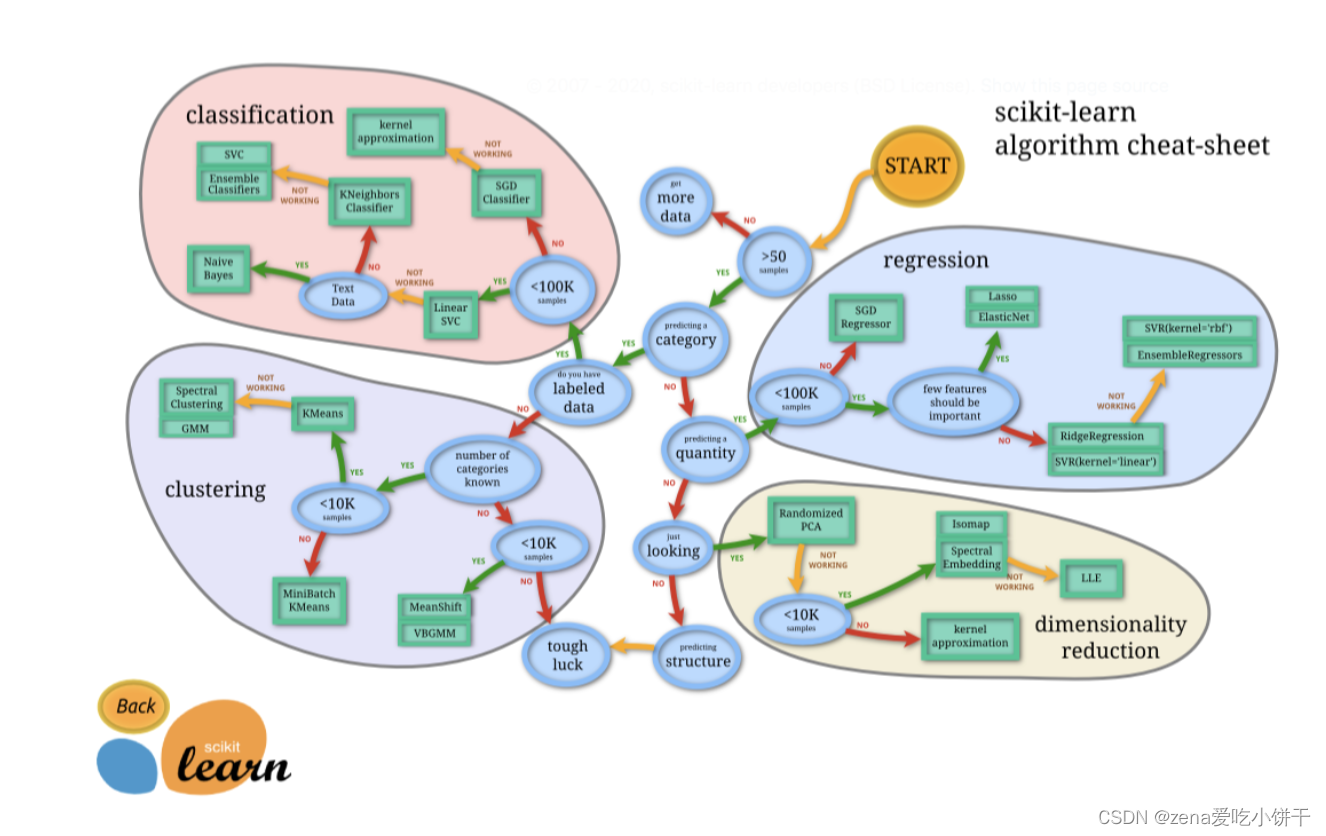
Data & Tasks & Algorithms

1. data(explain with case)
   - data point
   - feature
   - feature extraction/engineering

2. task(figure: overview of ml tasks)
   - regression
   - classification
   - clustering
   - dimensonality reduction
   < Different tasks have different loss functions, refer to 1.3–Function >

3. algorithm
   - supportvectormachines(SVMs)
   - nearestneighbours
   - random forest
   - k means
   - matrix factorisaion/autoencoder
   - …

1.3 Deep Learning

Definition(supervised & unsupervised)

Deep learning solves Problems by employing neural networks(artificial neural networks), functions constructed by composing alternatingly affine and (simple) non-linear functions.

Task

• prediction
• classification
• image recognition
• speech recognition and synthesis
• simulation
• optimal decision making
• …
  

Applications in Finance

• detect fraud
• machine read cheques
• perform credit scoring

Limits

• limited explainability of deep learning
• black-box nature of neural networks

Function

f = ( f 1 , . . . , f O ) : R I → R O f =(f_1,...,f_O):R^I →R^O f=(f1​,...,fO​):RI→RO

• inputs
  x 1 , . . . , x I x_1,...,x_I x1​,...,xI​   ($I\in \mathbb{N}$)
• outputs
  f 1 ( x 1 , . . . , x I ) , . . . , f O ( x 1 , . . . , x I ) f_1(x_1,...,x_I),..., f_O(x_1,...,x_I ) f1​(x1​,...,xI​),...,fO​(x1​,...,xI​)   ($O\in \mathbb{N}$)
• loss function
  L ( f ) : = 1 I ∑ i = 1 I l ( f i ^ , f i ) L(f):=frac{1}{I}sum_{i=1}^Il(hat{f_i},f_i) L(f):=I1​∑i=1I​l(fi​^​,fi​)   (e.g. squared loss, absolute loss)

1) Example

• Regression Problem: data fitting
• Binary Classification Problem:the direction of next price change//credit risk analysis

2) A Class of Functions Construction

• rich in the sense that it encompasses “almost any” reasonable functional relationship between the outputs and inputs;
• parameterised by a finite set of parameters,so that we can actually work with it numerically;
• able to cope with high-dimensional inputs and outputs.

3) Optimal $f$ Selection

• implementable numerically;
• efficient enough to be able to cope with large numbers of samples;
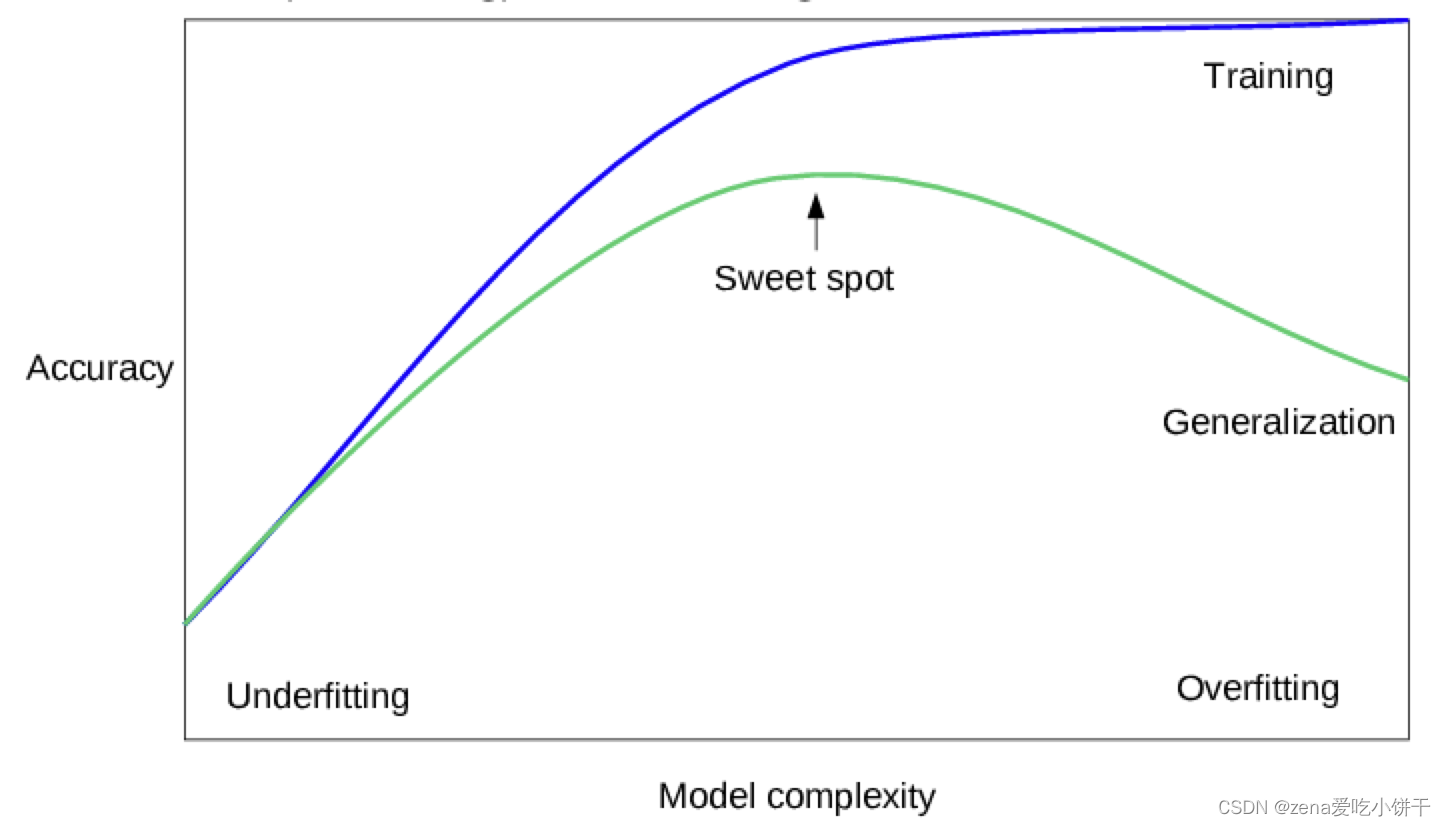
• able to avoid the pitfall of overfitting, that is, producing a function $f$ that performs well with the training data but poorly with other data.
  

4) Functions in Deep Learning

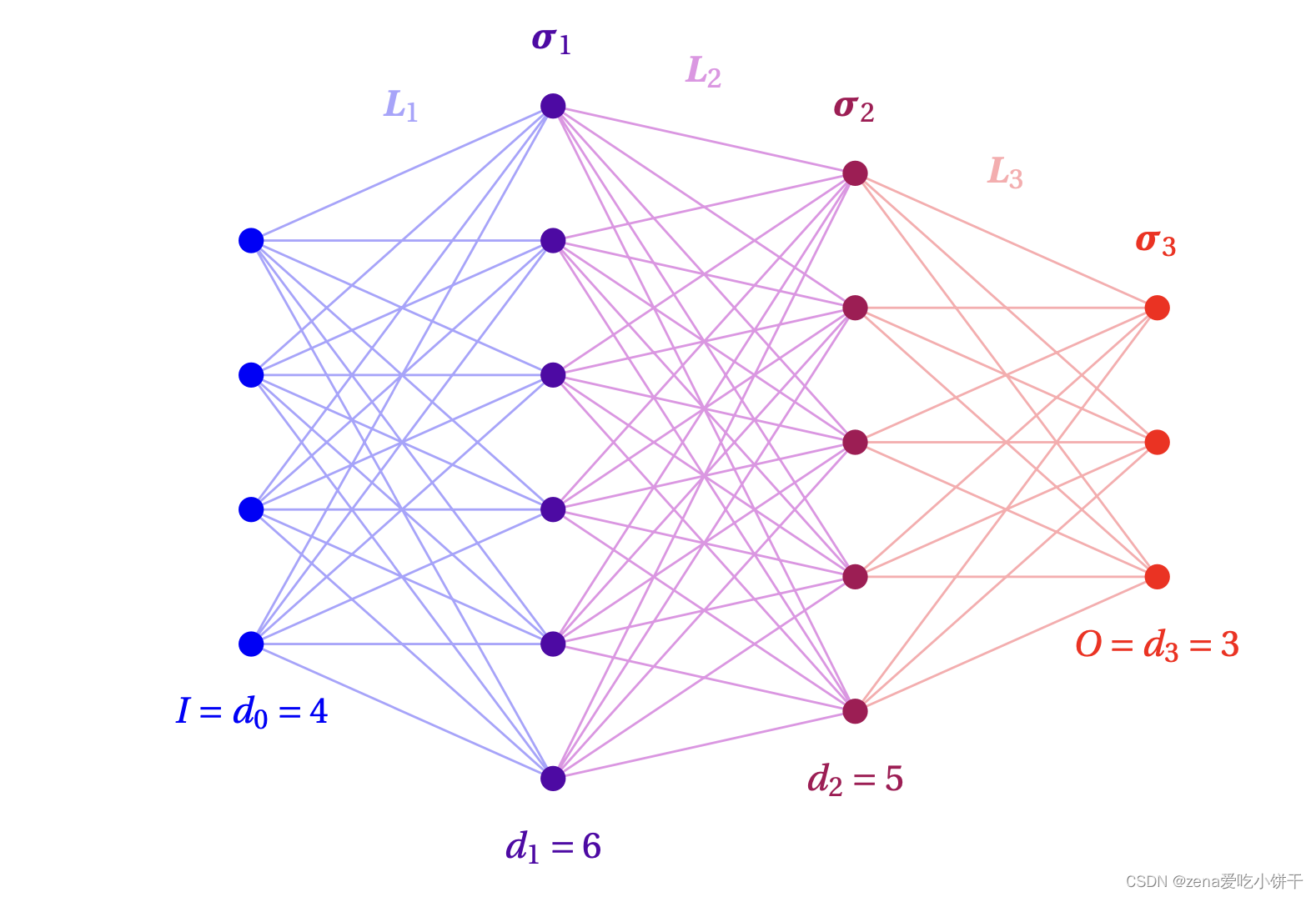
• Function: Affine FunctionActivation Function
  f = σ r ◦ L r ◦ ⋅ ⋅ ⋅ ◦ σ 1 ◦ L 1 : R I → R O f =σ_r ◦L_r ◦···◦σ_1◦L_1:R^I →R^O f=σr​◦Lr​◦⋅⋅⋅◦σ1​◦L1​:RI→RO
  where
  x = ( x 1 , . . . , x d i ) ∈ R d i x =(x_1,...,x_{d_i} )∈R_{d_i} x=(x1​,...,xdi​​)∈Rdi​​;
  L i : R d i − 1 → R d i L_i:R^{d_i-1} → R^{d_i} Li​:Rdi​−1→Rdi​, $\forall$$i\in \mathbb{N}$ is an affine function, transmiting d i − 1 d_{i−1} di−1​ signals to d i d_i di​ units or neurons;
  σ i ( x ) : = ( σ i ( x 1 ) , . . . , σ i ( x d i ) ) : R → R σ_i(x):=(σ_i(x_1),...,σ_i(x_{d_i} )):R→R σi​(x):=(σi​(x1​),...,σi​(xdi​​)):R→R is an activation function, transforming d i − 1 d_{i−1} di−1​ siginals.
  

  < satisfy the 2) requirement>
  < Since there is no specific data definition for the model, it’s super general to fit diverse data.>

• Optimal $f$:stochastic gradient descent (SGD)
  - the matrices and vectors parameterise its layers
  - a randomly drawn subset of samples(minibatch) is used
  - the gradient is computed using a form of algorithmic differentiation(backpropagation)

• Loss function
  generally absolute value of residual,but some others in particular

History of Deep Learning

• Heaviside function< problem sheet1>
  f ( x ; w , b ) : = H ( w ′ x + b ) , f(x;w,b) := H(w^′x +b), f(x;w,b):=H(w′x+b), where
  H ( x ) : = { 0 , x < 0 1 , x ≥ 0 H(x):=begin{cases} 0,quad x< 0 \[2ex] 1, quad xgeq0 end{cases} H(x):=⎩⎨⎧​0,x<01,x≥0​
• Artificial Neuron case
  
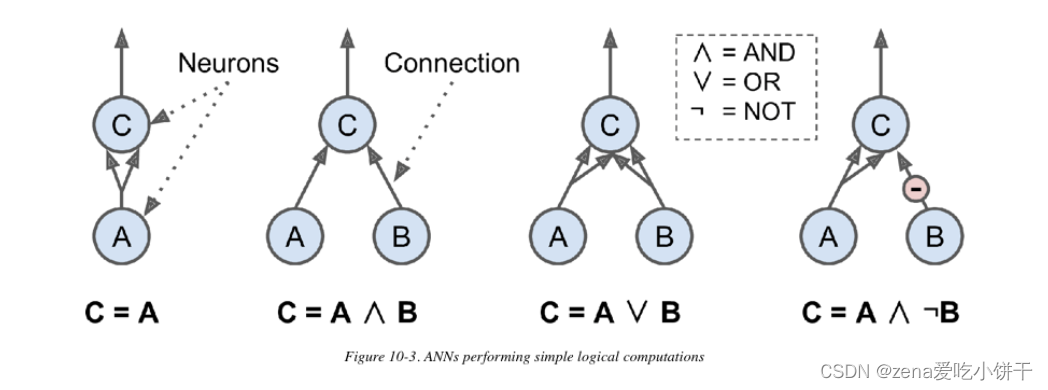
  - 1: if neuron A is activated, then neuron C gets activated as well (since it receives two input signals from neuron A); but if neuron A is off, then neuron C is off as well.
  - 2: (logical AND) Neuron C is activated only when both neurons A and B are activated (a single input signal is not enough to activate neuron C).
  - 3: (logical OR) Neuron C gets activated if either neuron A or neuron B is activated (or both).
  - 4: (logical NOT) Neuron C is activated only if neuron A is active and neuron B is off. If A is active all the time, then neuron C is active when neuron B is off, and vice versa.