机器学习：使用PCA简化数据

文章目录

使用场景

我们通过电视看实况足球，电视显示屏有100万个像素点，球所占的点数为100个。人眼会把显示器上的百万像素转为三维图像，在图中可以捕捉球的运动轨迹，此时就已经实现通过“降维”获取关键数据的目的。

主成分分析（Principal component analysis）

作用和原理：找出主要特征进行分析，主成分是原始数据的线性组合，通过最大化数据方差来确定，比如第一个主成分解释了数据中最大的方差，第二个主成分解释了剩余数据中最大的方差，以此类推。
方差：用来表述数据的离散程度，一个变量的方差可以视为它每个元素与元素均值的差的平方和的均值，为便于处理，可以想办法把均值化成0（u=0），即：
$frac{1}{m}sum_{i=1}^{m}(a_i-μ)^2$
举例：假设我有一个包含房屋面积，房价和使用年限的数据集，现在我想要了解这些特征之间的关系，并找到一种简洁的表示方式。首先，用PCA进行降维，假设得到了两个主成分，第一个是房屋面积，它能反映房屋的整体大小以及宜居人数，第二个是房价，他能影响消费者的购买方式（全额/按揭）。然后，把原始数据集投影到这俩成分里，得到一个新的低维表示（尽可能在不影响结果的前提下实现3维降到2维）。最后，用得到的两个主成分重新分析数据，绘制主成分直接的关系图以了解房屋面积，房价对使用年限的影响；还可以用这些特征做聚类分析，找到具有相似特征的房屋群组。
优点：通过给数据降维，去除冗余信息，减少计算量；
缺点：PCA假定数据之间存在线性q关系，如果数据是非线性的（比如图像曲线是个正弦函数），效果可能就不怎么样。并且，PCA对数据的“单位”比较敏感，如果数据的衡量尺度不一，容易导致结果出现偏差。比如有一个身高-体重数据集，前者单位可以是cm，后者可以是kg，如果不对数据做归一化，PCA就可能给身高更大的权重（假设身高175cm，体重70kg）。

实验：对半导体数据（590个特征）进行降维处理

代码网址：https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/13.PCA/pca.py
处理的数据类型如下所示
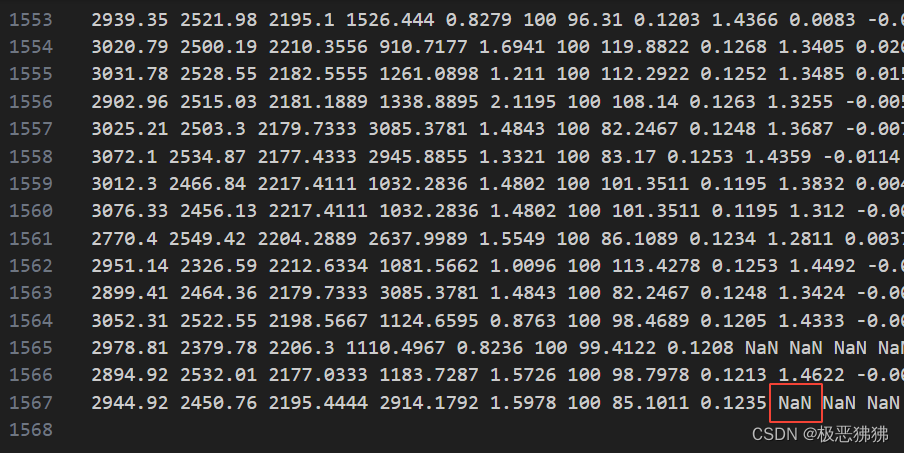
在这里插入图片描述
其中有一部分代码需要修改，replaceNanWithMean函数是为了把数据里的NaN（Not a Number）以各个特征的平均值来替换，原代码如下：

def replaceNanWithMean(): 
    datMat = loadDataSet('secom.data', ' ')
    numFeat = shape(datMat)[1]
    for i in range(numFeat):
        meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) #values that are not NaN (a number)
        datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal  #set NaN values to mean
    return datMat

报错结果：
在这里插入图片描述

修改后的代码如下：

def replaceNanWithMean():
    datMat = genfromtxt('secom.data', delimiter=' ', dtype=float)
    numFeat = datMat.shape[1]
    for i in range(numFeat):
        nonNanIndices = where(~isnan(datMat[:, i]))[0]
        nanIndices = where(isnan(datMat[:, i]))[0]
        meanVal = mean(datMat[nonNanIndices, i])
        datMat[nanIndices, i] = meanVal
    return datMat

代码解析：在原来的代码里，作者用自己定义的 $l o a d D a t a s S e t$ 函数读取数据，将所有的数据都解析为浮点数，但数据里的NaN并不是数值，我觉得可能是数据类型不同导致的错误。修改后的代码用到 $g e n f ro m t x t$ 函数，从文本文件中加载数据，创建一个numpy数组，读取数据集的列数并遍历每一列，用 $w h ere$ 和 $i s nan$ 函数找出Nan和非NaN的索引，分别记录。计算出所有非NaN的均值，再把NaN替换为均值，这样就不会出现报错。
实验解析：尝试输出矩阵的特征值，发现有一部分值是0，如下图所示。用线代的角度来看，应该可以理解为这个矩阵向量可以由其他特征向量线性组合得到，所以590个特征中，大部分的特征意义不大，可以被压缩掉。
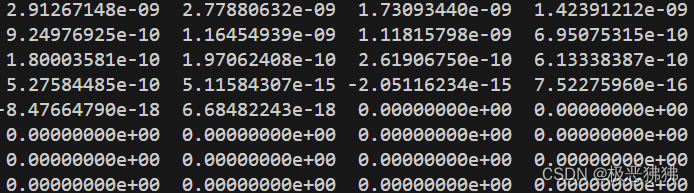
在这里插入图片描述
实验结果如下：

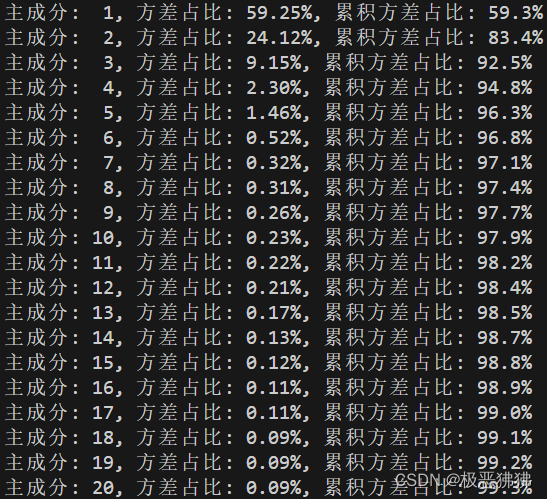
算法每次挑选方差最大的特征加入主成分列表，累计方差逐渐增加。在作者的代码里，设定20个主成分就可以描述器件特性。但看实验结果不难发现，当主成分数量增大到13个的时候，累计方差的增大速率就出现了明显的下降趋势，所以这个数值也是可以再做修改的。