2023华为OD机试真题【区间交叠/贪心算法】【Python Java】

题目描述

给定坐标轴上的一组线段，线段的起点和终点均为整数并且长度不小于1，请你从中找到最少数量的线段，这些线段可以覆盖住所有线段。

输入描述
第一行输入为所有线段的数量，不超过10000，后面每行表示一条线段，格式为”x,y”，
x和y 分别表示起点和终点，取值范围是[-10^5 ，10^5]。
输出描述

最少线段数量，为正整数。
输入
3
1,4
2,5
3,6
输出
2

题意解读

首先，用示例来理解题意：现在有三条线段：

一号线段：起点1，终点4；

二号线段：起点2，终点5；

三号线段：起点3，终点6；

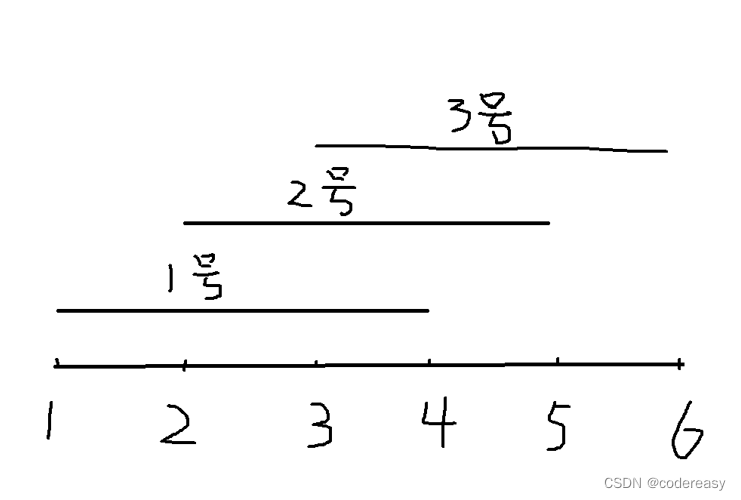
我们要从这三条线段中，选出若干条线段，覆盖1~6整个区间。

比如，我们可以选择 一号、二号、三号。一号覆盖 1~4 ，二号覆盖 2~5，三号覆盖3~6，三条线段加起来可以覆盖1~6整个区间。但是，题目要求尽可能选择少的线段。因此，我们只用选择一号、三号，也能覆盖1~6整个区间。所以，答案就是选择2条线段（即一号、三号）。

解题思路

这是一道典型的贪心算法，贪心策略如下：

首先，将所有线段按起点从小到大排序。

然后遍历排序后的线段，每遍历到一个线段（我们称当前正在遍历的线段为current线段），找出后面的线段中左端点小于等于current线段的右端点的所有线段（我们称之为备选线段），找出备选线段中右端点最大的一个线段maxLine。下一步遍历maxLine。

不断重复以上操作，直到覆盖完整个长度为m的区间，就能得到最少的线段数。

视频讲解

示例代码（Java版本）

import java.util.LinkedList;
import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        
        int n = sc.nextInt();
        sc.nextLine();
        
        Integer[][] segs = new Integer[n][];
        for (int i = 0; i < n; i++) {
            segs[i] = getSeg(sc.nextLine());
        }
        
        sort(segs);

        LinkedList<Integer[]> coverSegs = cover(segs);

        System.out.println(coverSegs.size());
    }

    private static Integer[] getSeg(String line) {
        String[] parts = line.split(",");
        return new Integer[]{Integer.parseInt(parts[0]), Integer.parseInt(parts[1])};
    }

    private static void sort(Integer[][] segs) {
        Arrays.sort(segs, (a, b) -> a[0].compareTo(b[0]));
    }

    private static LinkedList<Integer[]> cover(Integer[][] segs) {
        LinkedList<Integer[]> stack = new LinkedList<>();
        stack.add(segs[0]);

        for (int i = 1; i < segs.length; i++) {
            while (true) {
                if (stack.isEmpty()) {
                    stack.add(segs[i]);
                    break;
                }
                
                Integer[] top = stack.getLast();
                Integer[] cur = segs[i];

                if (cur[0] <= top[0]) {
                    if (cur[1] <= top[0]) {
                        break;
                    } else if (cur[1] < top[1]) {
                        break;
                    } else {
                        stack.removeLast();
                    }
                } else if (cur[0] < top[1]) {
                    if (cur[1] <= top[1]) {
                        break;
                    } else {
                        stack.add(new Integer[]{top[1], cur[1]});
                        break;
                    }
                } else {
                    stack.add(cur);
                    break;
                }
            }
        }

        return stack;
    }
}

示例代码（Python版本）

def get_segs(line):
    parts = line.split(",")
    return [int(parts[0]), int(parts[1])]

def sort_segs(segs):
    return sorted(segs, key=lambda x: x[0])

def cover(segs):
    stack = [segs[0]]

    for i in range(1, len(segs)):
        while True:
            if not stack:
                stack.append(segs[i])
                break

            top = stack[-1]
            cur = segs[i]

            if cur[0] <= top[0]:
                if cur[1] <= top[0]:
                    break
                elif cur[1] < top[1]:
                    break
                else:
                    stack.pop()
            elif cur[0] < top[1]:
                if cur[1] <= top[1]:
                    break
                else:
                    stack.append([top[1], cur[1]])
                    break
            else:
                stack.append(cur)
                break

    return stack

if __name__ == '__main__':
    n = int(input())
    segs = [get_segs(input()) for _ in range(n)]
    sorted_segs = sort_segs(segs)
    cover_segs = cover(sorted_segs)

    print(len(cover_segs))