逻辑回归算法
活动地址:CSDN21天学习挑战赛
概念
引例
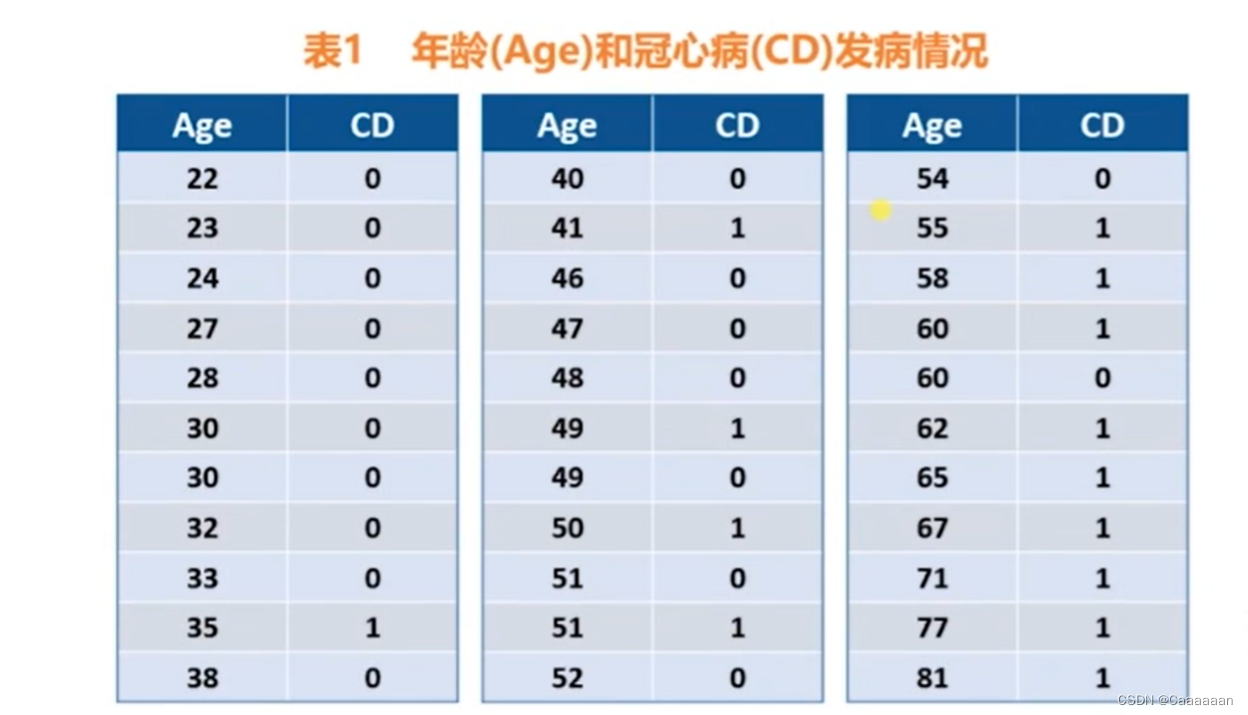
我们无法做到,根据年龄和是否的冠心病的散点图,得到回归
——因此,我们将年龄这个连续值和是否的冠心病进行转换
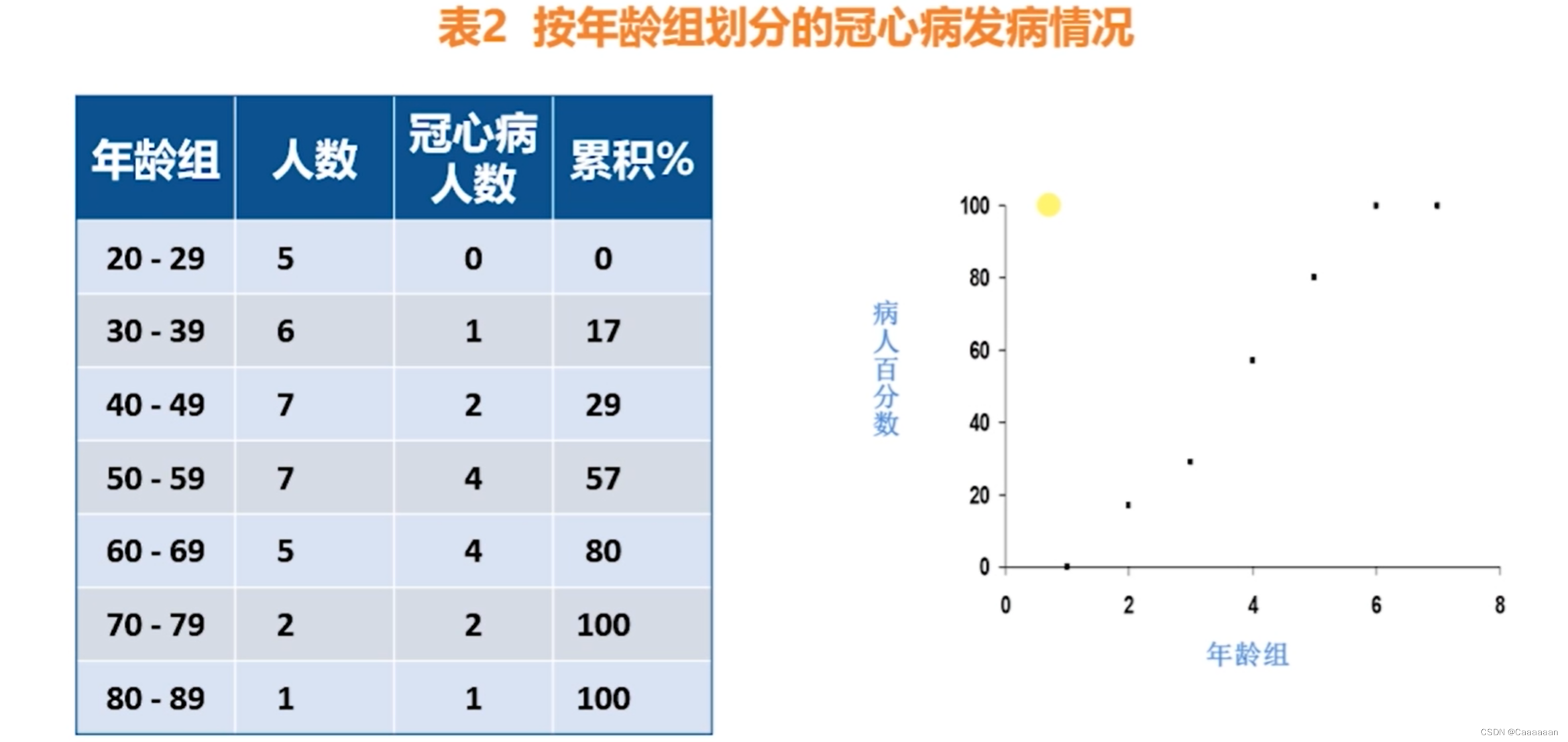
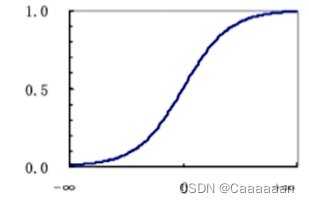
——然后,我们就能得到逻辑斯特回归曲线
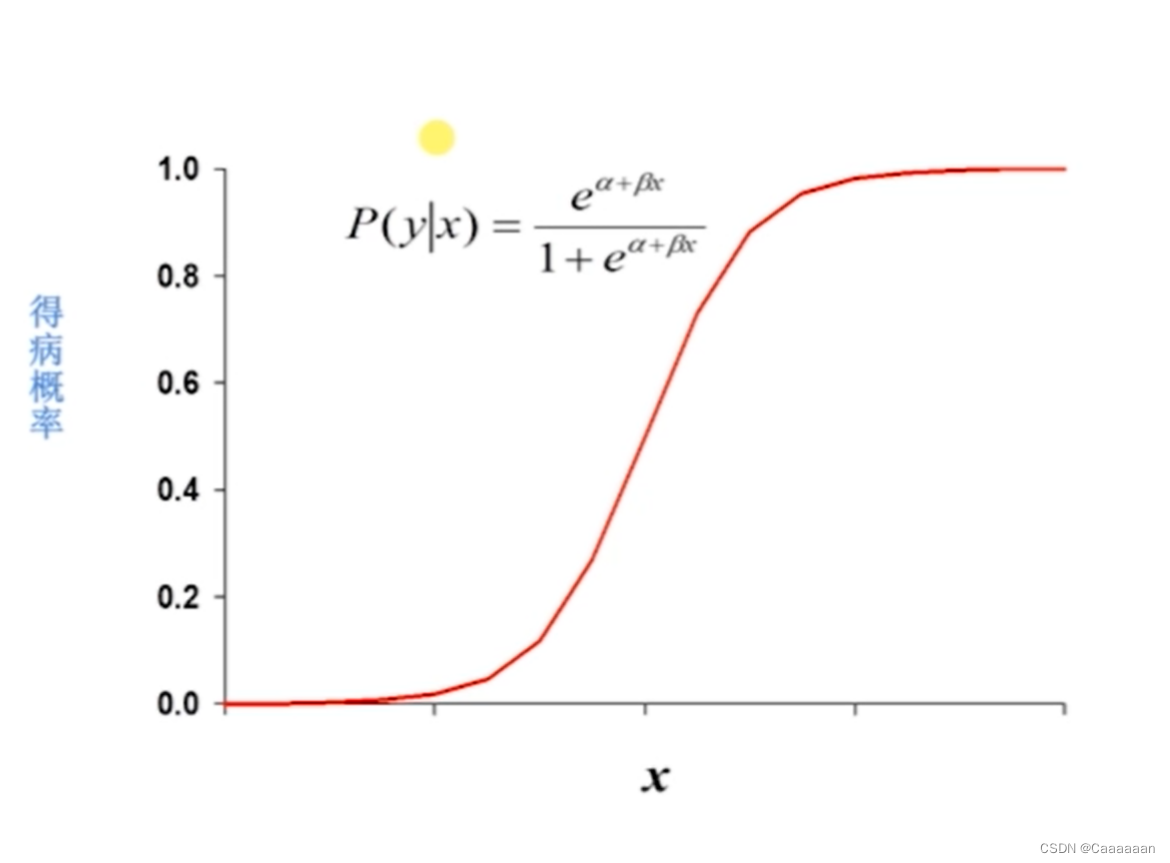
定义
背景:1838年由比利时学者Verhulst首次提出;1920年美国学者Bearl & Reed在研究果蝇的繁殖中发现和使用该函数,并在人口估计和预测中推广使用
l o g i s t i c 函数的值域为 [ 0 , 1 ] f ( x ) = e x 1 + e x 用 p i = P ( y i = 1 ∣ x i 1 , x i 2 , . . . , x i p ) logistic函数的值域为[0,1]\ f(x)=frac{e^x}{1+e^x}\ 用 p_i=P(y_i=1|x_{i1},x_{i2},...,x_{ip}) logistic函数的值域为[0,1]f(x)=1+exex用pi=P(yi=1∣xi1,xi2,...,xip)
作为因变量,得到 l o g i s t i c 回归模型 p i = e x p ( α + β 1 x i 1 + β 2 x i 2 + . . . + β p x i p ) 1 + e x p ( α + β 1 x i 1 + β 2 x i 2 + . . . + β p x i p ) l n p i 1 − p i = α + β 1 x i 1 + β 2 x i 2 + . . . + β p x i p p i 就是患病的概率 作为因变量,得到logistic回归模型\ p_i=frac{exp(alpha+beta_1x_{i1}+beta_2x_{i2}+...+beta_px_{ip})}{1+exp(alpha+beta_1x_{i1}+beta_2x_{i2}+...+beta_px_{ip})}\ lnfrac{p_i}{1-p_i}=alpha+beta_1x_{i1}+beta_2x_{i2}+...+beta_px_{ip}\ p_i就是患病的概率 作为因变量,得到logistic回归模型pi=1+exp(α+β1xi1+β2xi2+...+βpxip)exp(α+β1xi1+β2xi2+...+βpxip)ln1−pipi=α+β1xi1+β2xi2+...+βpxippi就是患病的概率
逻辑回归特点:线性分类器
最简单的逻辑回归就是线性分类器,如左图
而如右图的,则是非线性的分类器
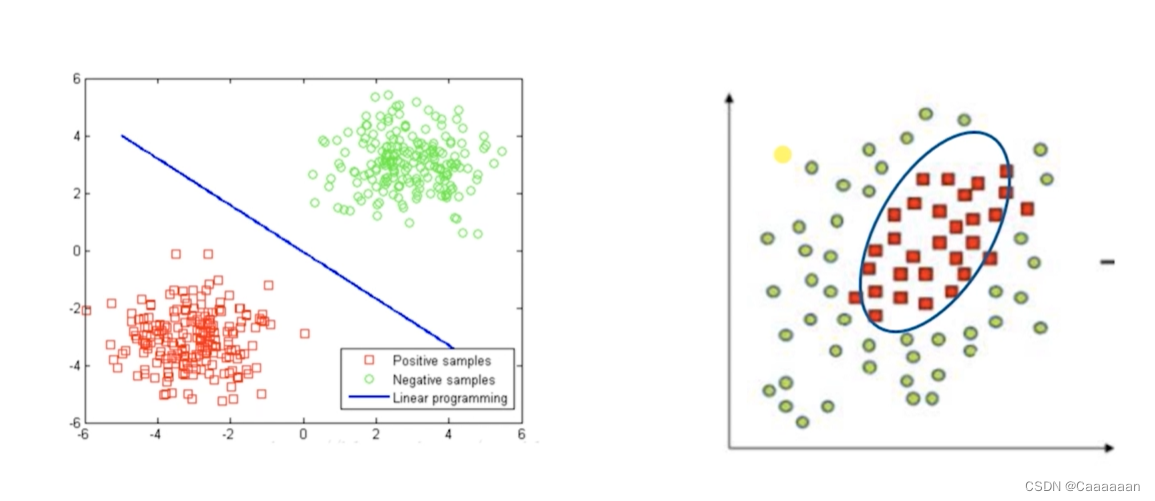
——为什么是逻辑回归是线性分类器
∙
逻辑斯特回归函数:
l
n
p
i
1
−
p
i
=
α
+
β
1
x
i
1
+
β
2
x
i
2
+
.
.
.
+
β
p
x
i
p
L
o
g
i
t
(
l
o
g
i
s
t
i
c
p
r
o
b
a
b
i
l
i
t
y
u
n
i
t
)
变换
:
定义:
L
o
g
i
t
(
p
i
)
=
l
n
p
i
1
−
p
i
∙
得到
L
o
g
i
t
(
p
i
)
=
α
+
β
1
x
i
1
+
β
2
x
i
2
+
.
.
.
+
β
p
x
i
p
+
ε
i
L
o
g
i
t
变换的特点:
L
o
g
i
t
(
p
i
)
=
l
n
p
i
1
−
p
i
∈
(
0
,
+
∞
)
[
正类
]
L
o
g
i
t
(
p
i
)
=
l
n
p
i
1
−
p
i
∈
(
−
∞
,
0
)
[
负类
]
bullet 逻辑斯特回归函数:\ lnfrac{p_i}{1-p_i}=alpha+beta_1x_{i1}+beta_2x_{i2}+...+beta_px_{ip}\ Logit(logistic,,probability,,unit)变换:\ 定义:Logit(p_i)=lnfrac{p_i}{1-p_i}\ bullet 得到Logit(p_i)=alpha+beta_1x_{i1}+beta_2x_{i2}+...+beta_px_{ip}+varepsilon_i\ Logit变换的特点:\ Logit(p_i)=lnfrac{p_i}{1-p_i}in (0,+infty)[正类]\ Logit(p_i)=lnfrac{p_i}{1-p_i}in (-infty,0)[负类]\
∙逻辑斯特回归函数:ln1−pipi=α+β1xi1+β2xi2+...+βpxipLogit(logisticprobabilityunit)变换:定义:Logit(pi)=ln1−pipi∙得到Logit(pi)=α+β1xi1+β2xi2+...+βpxip+εiLogit变换的特点:Logit(pi)=ln1−pipi∈(0,+∞)[正类]Logit(pi)=ln1−pipi∈(−∞,0)[负类]
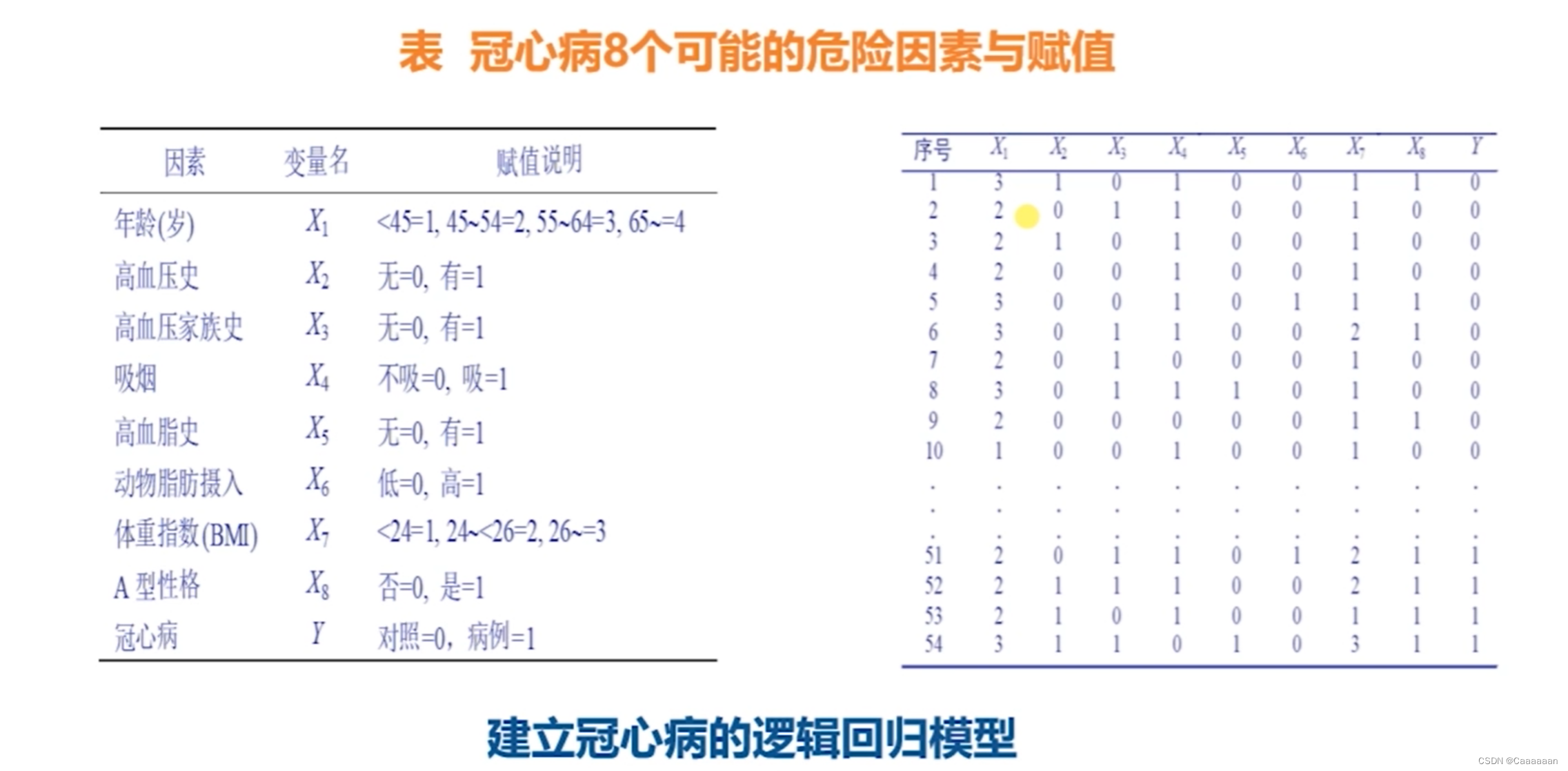
优势比OR
l n P 1 − P = β 0 + β 1 X 1 + β 2 X 2 + . . . + β m X m = l o g i t P lnfrac{P}{1-P}=beta_0+beta_1X_1+beta_2X_2+...+beta_mX_m=logitP ln1−PP=β0+β1X1+β2X2+...+βmXm=logitP
模型参数意义:
-
常数项 β 0 beta_0 β0
表示暴露剂量为0时个体发病与不发病概率之比的自然对数
-
回归系数 β j ( j = 1 , 2 , . . . , m ) beta_j(j=1,2,...,m) βj(j=1,2,...,m)
表示自变量改变一个单位时logitP的改变量
-
流行病学衡量危险因素作用大小的比数比例指标
-
计算公式为: O R j = P 1 / ( 1 − P 1 ) P 0 / ( 1 − P 0 ) 计算公式为:\ OR_j=frac{P_1/(1-P_1)}{P_0/(1-P_0)}\ 计算公式为:ORj=P0/(1−P0)P1/(1−P1)
-
表示自变量变化以后,发病概率的变化情况
-
比如,自变量=0时,发病概率是 P 0 1 − P 0 frac{P_0}{1-P_0} 1−P0P0
自变量=1时,发病概率是 P 1 1 − P 1 frac{P_1}{1-P_1} 1−P1P1
因此优势比OR反映的是发病概率的变化情况
-
式中 P 0 P_0 P0和 P 1 P_1 P1分别表示在同一危险因素 X j X_j Xj取值为 c 0 c_0 c0及 c 1 c_1 c1时的发病概率
O R j OR_j ORj称作多变量调整后的优势比,表示扣除了其他自变量影响后危险因素的作用
即只考虑一个变量,对整个发病的影响
与 l o g i s t i c P 的关系: ∙ 对比某一危险因素两个不同暴露水平 X j = c 0 与 X j = c 1 的发病情况 假定其他因素的水平相同,则优势比的自然对数为: l n O R j = l n [ P 1 / ( 1 − P 1 ) P 0 / ( 1 − P 0 ) ] = l o g i t P 1 − l o g i t P 0 = ( β 0 + β j c 1 + ∑ t ≠ j m β t X t ) − ( β 0 + β j c 0 + ∑ t ≠ j m β t X t ) = β j ( c 1 − c 0 ) 与logisticP的关系:\ bullet 对比某一危险因素两个不同暴露水平X_j=c_0与X_j=c_1的发病情况\ 假定其他因素的水平相同,则优势比的自然对数为:\ lnOR_j=ln[frac{P_1/(1-P_1)}{P0/(1-P_0)}]=logitP_1-logitP_0\ =(beta_0+beta_jc_1+sum_{tneq j}^mbeta_tX_t)-(beta_0+beta_jc_0+sum_{tneq j}^mbeta_tX_t)\ =beta_j(c_1-c_0) 与logisticP的关系:∙对比某一危险因素两个不同暴露水平Xj=c0与Xj=c1的发病情况假定其他因素的水平相同,则优势比的自然对数为:lnORj=ln[P0/(1−P0)P1/(1−P1)]=logitP1−logitP0=(β0+βjc1+t=j∑mβtXt)−(β0+βjc0+t=j∑mβtXt)=βj(c1−c0)
-
即得 O R j = e x p [ β j ( c 1 − c 0 ) ] OR_j=exp[beta_j(c_1-c_0)] ORj=exp[βj(c1−c0)]
-
若 X j = { 1 暴露 0 非暴露 , c 1 − c 0 = 1 若X_j= begin{cases} 1&暴露\ 0&非暴露 end{cases} ,c_1-c_0=1 若Xj={10暴露非暴露,c1−c0=1
则有 O R j = e x p β j β j { = 0 , O R j = 1 无作用 > 0 , O R j > 1 危险因子 < 0 , O R j < 1 保护因子 则有OR_j=expbeta_j\ beta_j begin{cases} =0,OR_j=1&无作用\ >0,OR_j>1&危险因子\ <0,OR_j<1&保护因子\ end{cases} 则有ORj=expβjβj⎩ ⎨ ⎧=0,ORj=1 >0,ORj>1<0,ORj<1无作用危险因子保护因子
优势比理解
在一个具有17个家庭的样本里,共有3家的收入为¥10000,5家的收入为¥11000,9家的收入为¥12000
在收入¥10000的家庭里,1个主妇不工作,2个主妇工作
在收入¥11000的家庭里,1个主妇不工作,4个主妇工作
在收入¥12000的家庭里,1个主妇不工作,8个主妇工作
| 收入 | 不工作 | 工作 | 总计 |
|---|---|---|---|
| 10 | 1 | 2 | 3 |
| 11 | 1 | 4 | 5 |
| 12 | 1 | 8 | 9 |
| 总计 | 3 | 14 | 17 |
- 主妇工作状态对收入的影响
| 收入 | 不工作 | 工作 | 工作概率 |
|---|---|---|---|
| 10 | 1 | 2 | 2/3 |
| 11 | 1 | 4 | 4/5 |
| 12 | 1 | 8 | 8/9 |
-
当X分别取10和11时:
O R j = 4 5 / ( 1 − 4 5 ) 2 3 / ( 1 − 2 3 ) = 4 / 2 = 2 OR_j=frac{frac{4}{5}/(1-frac{4}{5})}{frac{2}{3}/(1-frac{2}{3})}=4/2=2\ ORj=32/(1−32)54/(1−54)=4/2=2 -
当X分别取11和12时:
O R j = 8 9 / ( 1 − 8 9 ) 4 5 / ( 1 − 4 5 ) = 8 / 4 = 2 OR_j=frac{frac{8}{9}/(1-frac{8}{9})}{frac{4}{5}/(1-frac{4}{5})}=8/4=2\ ORj=54/(1−54)98/(1−98)=8/4=2
说明:
- 收入每增加一个单位,主妇工作的Odds增加到原来的2倍
- 说明收入对工作状态有正关系,收入越高,工作概率越高
- 在疾病检测中,说明一个因素越高,使得患病概率越高
逻辑回归正则化

针对同一个分类面,哪一个分类面更好
W在数值上越小越好,这样越能抵抗数据的扰动
——如何找到这个尽可能小的参数,因此引入我们的逻辑回归正则化
正则化表达式:
L
1
=
∑
i
=
0
m
∣
w
i
∣
L
2
=
∑
i
=
0
m
w
i
2
正则化表达式:\ L_1=sum_{i=0}^m|w_i|\ L_2=sum_{i=0}^mw_i^2
正则化表达式:L1=i=0∑m∣wi∣L2=i=0∑mwi2
- 重写误差函数lambda λ lambda λ是W的权重牺牲正确率来提高推广能力
E = ∑ i = 1 n ( y i − 1 1 + e − ( w 1 x i 1 + w 2 x i 2 + w 0 ) ) 2 + λ L 1 E = ∑ i = 1 n ( y i − 1 1 + e − ( w 1 x i 1 + w 2 x i 2 + w 0 ) ) 2 + λ L 2 E=sum_{i=1}^n(y_i-frac{1}{1+e^{-(w_1x_{i1}+w_2x_{i2}+w_0)}})^2+lambda L_1\ E=sum_{i=1}^n(y_i-frac{1}{1+e^{-(w_1x_{i1}+w_2x_{i2}+w_0)}})^2+lambda L_2\ E=i=1∑n(yi−1+e−(w1xi1+w2xi2+w0)1)2+λL1E=i=1∑n(yi−1+e−(w1xi1+w2xi2+w0)1)2+λL2
- 惩罚项:若学习到大权值使得误差小,但是再加上正则化式子以后使得上面E值表达
- 因此,最小化E值使得求解的权值尽可能的相对较小
一个有趣的结论:
- L 1 L_1 L1倾向于使得w要么取1,要么取0——稀疏编码
- L 2 L_2 L2倾向于使得w整体偏小——岭回归
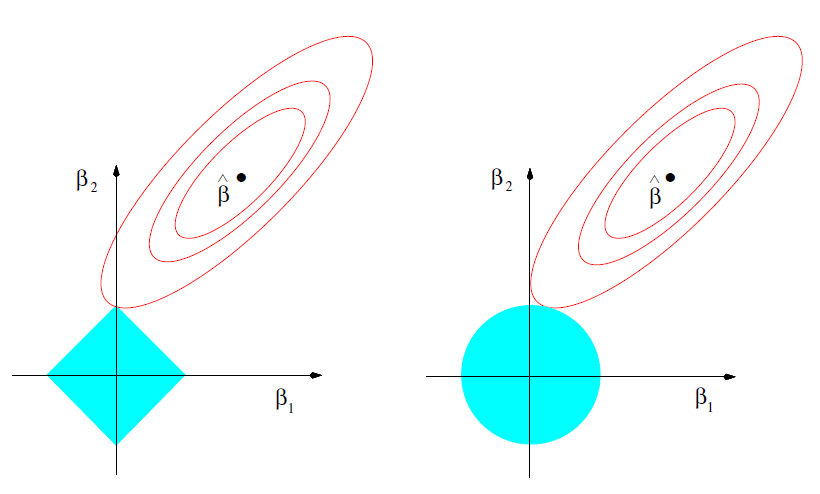
适用场景
-
L 1 L_1 L1适合降低维度
-
L 2 L_2 L2也称为岭回归,有很强的概率意义
逻辑回归数值优化
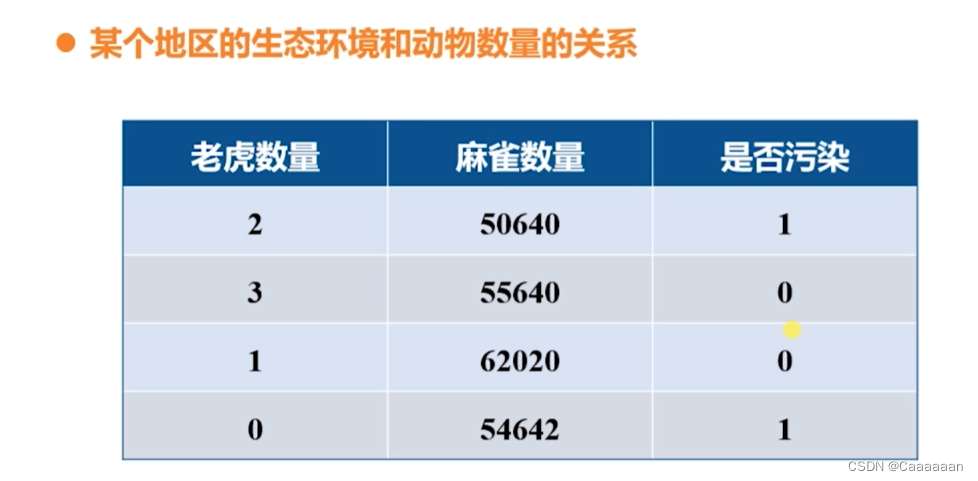
- 各个维度的输入如果在数值上差异很大,比如上表中老虎数量和麻雀数量,那么会引起正确的W在各个维度上数值差异很大
- 找寻W的时候,对各个维度的调整基本上是按照同一个数量级来进行调整的
——回顾到数据预处理学习的Z-score规范化
逻辑回归模型
-
梯度下降法的选择
-
两种梯度:
- SGD
- L-BFGS
L-BFGS为SGD的优化方法,它的训练速度比SGD快
| 数值归一化 | 正则化 | 梯度下降法 | 分类个数 | 数据选择 | |
|---|---|---|---|---|---|
| L-BFGS | 需要均值归一化,算法融入方差归一化 | 支持L2正则化 | L-BFGS(收敛快,考虑二阶导数) | 支持多分类 | 加载所有数据都参与训练 |
| SGD | 不归一化,需要专门在外面进行归一化 | 支持L1,L2 | SGD | 不支持多分类 | 随机从训练集选取(支持 M i n i B a t c h F r a c t i o n MiniBatchFraction MiniBatchFraction) |
-
logistic回归对噪声数据敏感
-
分类和回归都可用于预测,分类的输出是离散的类别值,而回归的输出是连续数值