代码随想录Day23 回溯算法 LeetCode T93 复原ip地址
LeetCode T93 复原ip地址


题目链接 :
题目思路:
首先我们可以进行一次剪枝,首先正确的ip地址要在12位,所以如果字符串的长度大于12我们就直接进行剪枝,接下来进行回溯函数的逻辑书写,我们知道正确的ip地址之间是用.分割的,当.的数量达到3个的时候也就是我们开始收集结果的时候了,别忘了收集结果的时候也要添加最后一段字符串,显而易见我们这里回溯的参数就有了,一个pointNum来记录我们的'.'字符个数,我们可以选择更快避免拷贝的StringBuilder ,这里我们就直接对字符串s进行修改
1.回溯函数参数
public void backtracking(String s,int startIndex,int pointNum)2.终止条件
if(pointNum == 3) { if(isValid(s,startIndex,s.length()-1)) { result.add(s); return; } }3.for循环
for(int i = startIndex;i<s.length();i++) { if(isValid(s,startIndex,i)) { s = s.substring(0,i+1)+"."+s.substring(i+1); pointNum++; backtracking(s,i+2,pointNum); pointNum--; s = s.substring(0,i+1) + s.substring(i+2); } else { break; } }4.isVaild函数
这里笔者犯了一个小错误,我误将'0'字符的ascll码强转为了int类型,导致将字符转整形失败了
char a = '0'; int b = (int)a; //48 int c = a - '0';//0public boolean isValid(String s,int begin,int end) { if(begin>end) { return false;//没有元素 } if(s.charAt(begin) == '0' && begin != end) { return false;//首位为0并且不是唯一一位,不符合 } int num = 0; for(int i = begin;i<=end;i++) { if(s.charAt(i)>'9' || s.charAt(i)<'0') { return false;//每个字符不再'0-9'之间 } num = num*10+(int)s.charAt(i)-48; if(num>255) { return false;//不符合IP地址 } } return true; }
题目代码:
lass Solution {
List<String> result = new ArrayList<>();
public List<String> restoreIpAddresses(String s) {
if(s.length()>12)
{
return result;
}
backtracking(s,0,0);
return result;
}
public void backtracking(String s,int startIndex,int pointNum)
{
//终止条件
if(pointNum == 3)
{
if(isValid(s,startIndex,s.length()-1))
{
result.add(s);
return;
}
}
//for循环
for(int i = startIndex;i<s.length();i++)
{
if(isValid(s,startIndex,i))
{
s = s.substring(0,i+1)+"."+s.substring(i+1);
pointNum++;
backtracking(s,i+2,pointNum);
pointNum--;
s = s.substring(0,i+1) + s.substring(i+2);
}
else
{
break;
}
}
}
public boolean isValid(String s,int begin,int end)
{
if(begin>end)
{
return false;
}
if(s.charAt(begin) == '0' && begin != end)
{
return false;
}
int num = 0;
for(int i = begin;i<=end;i++)
{
if(s.charAt(i)>'9' || s.charAt(i)<'0')
{
return false;
}
num = num*10+(int)s.charAt(i)-48;
if(num>255)
{
return false;
}
}
return true;
}
}LeetCode T78 子集

题目思路
这题的思路很简单,直接照搬回溯的代码模板即可,我们将模板的思路再过一遍
这里我们只需要创建一个result来保存结果,创建一个path来保存每一条正确的路径即可
这题我们要记录树的所有节点
1.回溯函数的参数
这里我们只需要一个nums数组和startIndex即可,确定每次开始的位置就可以
public void backtracking(int[] nums,int startIndex)2.终止条件
这里没有什么终止条件,只要startIndex不超过nums.length即可,当然有for循环帮我们限制,所以可以直接省略这个终止条件
3.一次搜索逻辑(for循环)
我们只需要加入一次path,递归再回溯即可
for(int i = startIndex;i<nums.length;i++) { path.add(nums[i]); backtracking(nums,i+1); path.remove(path.size()-1); }
题目代码
class Solution {
List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int startIndex)
{
result.add(new ArrayList(path));
for(int i = startIndex;i<nums.length;i++)
{
path.add(nums[i]);
backtracking(nums,i+1);
path.remove(path.size()-1);
}
}
}LeetCode T90 子集II

题目思路
这题的思路和我们之前做过的组合问题II一样,我们都需要标记用过的元素来进行去重的操作,也就是我们之前说过的树层去重的操作
去重逻辑:
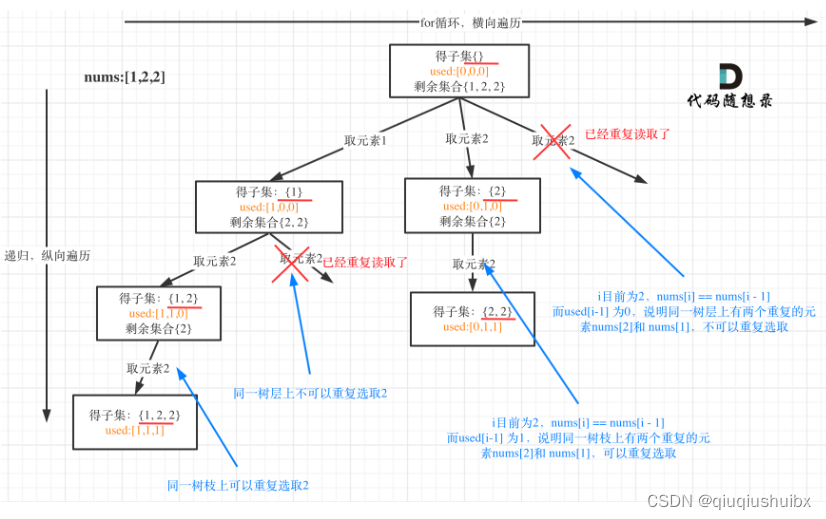
从上图我们知道,我们重复元素[1,1,2]中是不允许两个[1,2]同时存在的,所以在前两个元素相同时,我们可以舍弃第二个元素开始的递归,也就是舍弃第二条path,但是前提我们要先对这个数组进行排序,这样才能让两个相同元素靠在一起,我们才方便对两个元素中的后一个的递归进行舍弃,代码如下:
if(i>0 && nums[i] == nums[i-1]&& !used[i-1])1.递归参数
只需要nums数组和startIndex即可,由于其他变量都定义为全局变量了
public void backtracking(int[] nums,int startIndex)2.终止条件
由于这道题我们要计算空集在内,所以我们要先收集结果,这题的所有节点都是我们需要的结果
当startIndex超过我们nums的长度,那么我们就停止递归
if(startIndex>=nums.length) { return; }3.一次搜索逻辑
我们首先要判断该path是否有效,有就path记录,记录used数组,递归.path回溯
for(int i = startIndex;i<nums.length;i++) { if(i>0 && nums[i] == nums[i-1]&& !used[i-1]) { continue; } path.add(nums[i]); used[i] = true; backtracking(nums,i+1); path.remove(path.size()-1); used[i] = false; }
题目代码
class Solution {
boolean[] used;
List<Integer> path = new ArrayList<>();
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> subsetsWithDup(int[] nums) {
if(nums.length == 0)
{
result.add(path);
return result;
}
used = new boolean[nums.length];
Arrays.sort(nums);
backtracking(nums,0);
return result;
}
public void backtracking(int[] nums,int startIndex)
{
result.add(new ArrayList(path));
if(startIndex>=nums.length)
{
return;
}
for(int i = startIndex;i<nums.length;i++)
{
if(i>0 && nums[i] == nums[i-1]&& !used[i-1])
{
continue;
}
path.add(nums[i]);
used[i] = true;
backtracking(nums,i+1);
path.remove(path.size()-1);
used[i] = false;
}
}
}