Java 华为真题-猴子爬山

需求：

一天一只顽猴想去从山脚爬到山顶，途中经过一个有个N个台阶的阶梯，但是这猴子有一个习惯：每一次只能跳1步或跳3步，试问猴子通过这个阶梯有多少种不同的跳跃方式？

输入描述

输入只有一个整数N（0<N<=50）此阶梯有多少个台阶。

输出描述

输出有多少种跳跃方式（解决方案数）。

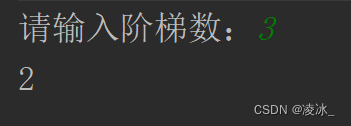
输入

3

输出

2

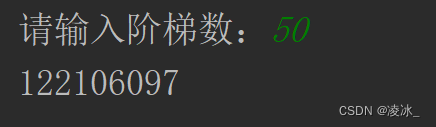
输入

50

输出

122106097

分析:

上山最后一步到达第50级台阶，完成上山，共有f（50）种不同的爬法，

到第50级之前位于哪一级呢？无非是位于第49级（上跳1级即到），有f（49）种；

或位于第48级（上跳3级即到），有f（48）种，于是：

f（50）=f（49）+f（47）
f（49）= f（48）+f（46）
f（48）= f（47）+f（45）
依次类推
以此类推，一般地有递推关系：

f（n）=f（n-1）+f（n-3）（n>3）
初始条件：

f（1）=1，即1=1；

f（2）=1，即2=1+1（注意：跳法中不允许直接跳2级）；

f（3）=2，即3=1+1+1，3=3；

故此递推设计比较简单，时间复杂度为O（n）

编码：

public class TestDump {
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        System.out.print("请输入阶梯数：");
        int num=scanner.nextInt();
        System.out.println(showF(num));
    }

    /**
     * 递归算法f(n) = f(n-1) + f(n-3);
     * f(1) =1;f(2) =1;f(3) = 2
     */
    public static long showF(int n) {
        if (n == 1 || n == 2) {
            return 1;
        }
        if (n == 3) {
            return 2;
        }
        return showF(n - 1) + showF(n - 3);
    }
}

需求：

分析:

编码：

效果：