运筹系列86:MIP问题的建模tips
1. Either-or constraint
添加辅助变量y。
比如
Either
3
x
1
+
2
x
2
≤
18
3x_1+2x_2 le 18
3x1+2x2≤18
or
x
1
+
4
x
2
≤
16
x_1+4x_2 le 16
x1+4x2≤16
可以用
3
x
1
+
2
x
2
≤
18
+
M
y
3x_1+2x_2 le 18+My
3x1+2x2≤18+My
x
1
+
4
x
2
≤
16
+
M
(
1
−
y
)
x_1+4x_2 le 16+M(1-y)
x1+4x2≤16+M(1−y)
来代替。
2. k out of N constraints must hold
类似上面,添加辅助变量
y
1
y_1
y1~
y
N
y_N
yN
从
f
1
(
.
.
.
)
≤
d
1
f_1(...)le d_1
f1(...)≤d1
…
f
N
(
.
.
.
)
≤
d
N
f_N(...)le d_N
fN(...)≤dN
变为
f
1
(
.
.
.
)
≤
d
1
+
M
y
1
f_1(...)le d_1+My_1
f1(...)≤d1+My1
…
f
N
(
.
.
.
)
≤
d
N
+
M
y
N
f_N(...)le d_N+My_N
fN(...)≤dN+MyN
Σ
1
N
y
i
=
N
−
k
,
y
i
Sigma_1^N y_i=N-k, y_i
Σ1Nyi=N−k,yi binary.
3. functions with N possible values
f ( x ) ∈ ( d 1 , . . . , d N ) f(x)in (d_1,...,d_N) f(x)∈(d1,...,dN)
添加辅助变量
y
1
y_1
y1~
y
N
y_N
yN
f
(
x
)
=
Σ
d
i
y
i
f(x)=Sigma d_iy_i
f(x)=Σdiyi
Σ
y
i
=
1
Sigma y_i=1
Σyi=1 (mutally exclusive alternatives)
4. fixed-charge problem
f
(
x
)
=
{
k
+
c
x
,
x
>
0
0
,
x
=
0
f(x)=begin {equation} begin{cases} k+cx, x>0\ 0,x=0\ end{cases} end {equation}
f(x)={k+cx,x>00,x=0
可以变为
f
(
x
)
=
c
x
+
k
y
f(x)=cx+ky
f(x)=cx+ky
x
≤
M
y
xle My
x≤My
y
y
y binary.
5. 综合例子

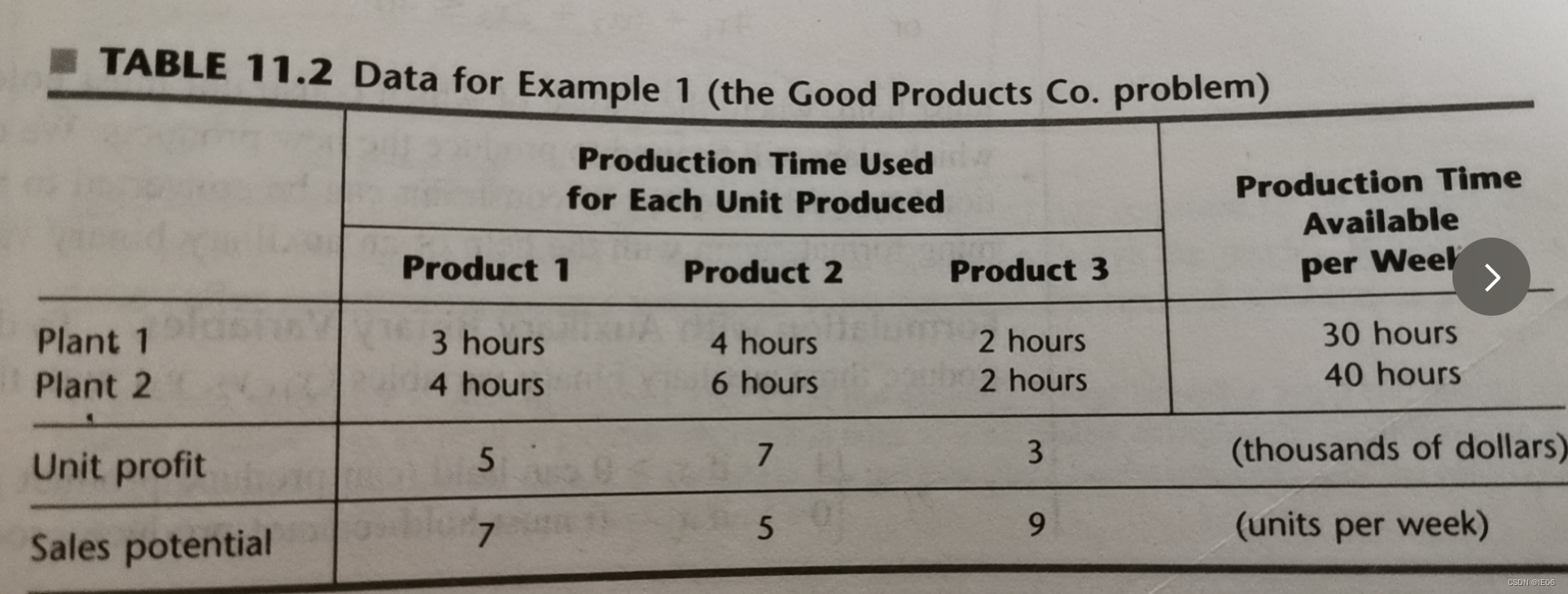
如果没有题目中的两个restriction,那么模型为:
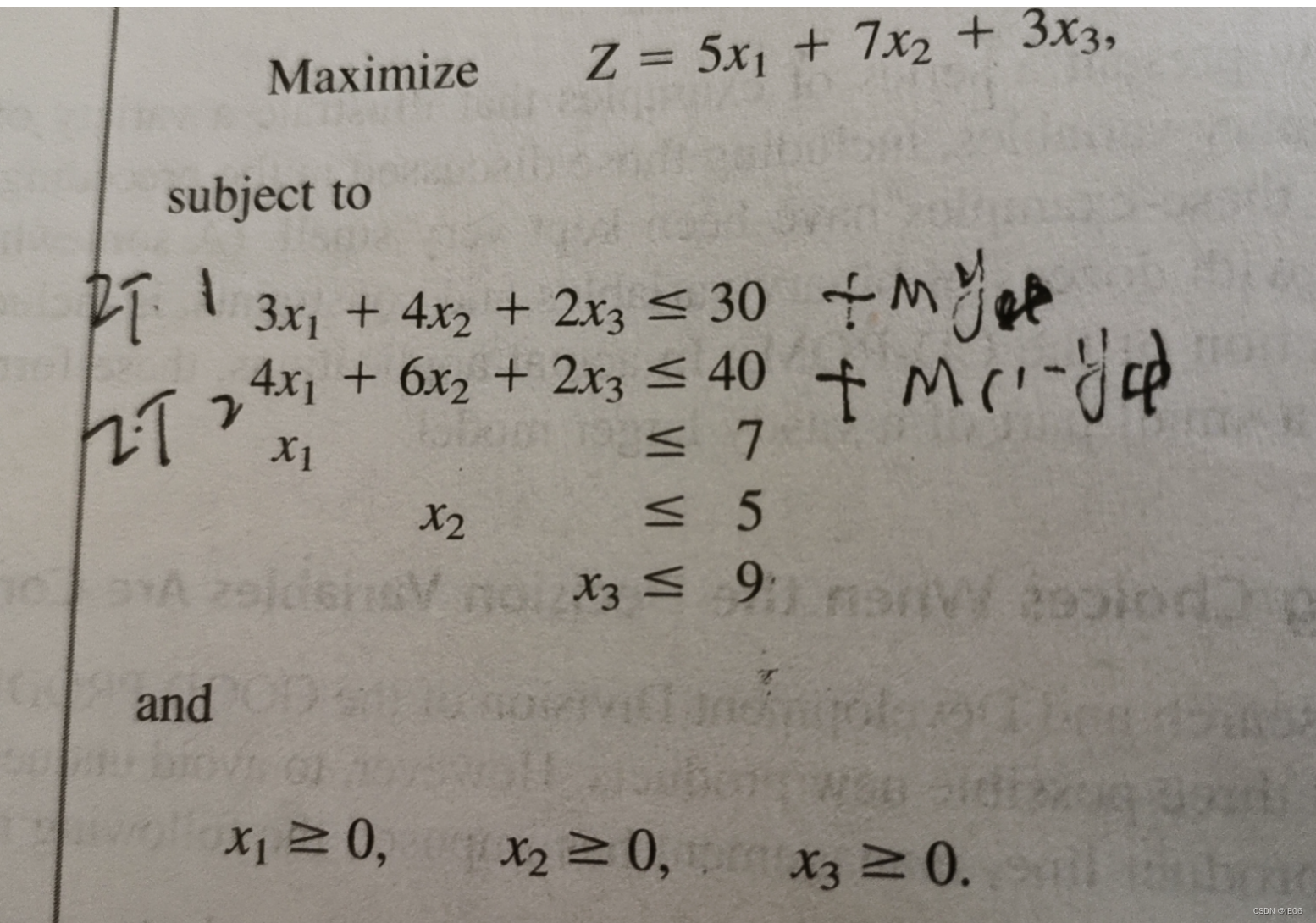
接下来我们看约束1,要求
x
1
,
x
2
,
x
3
x_1,x_2,x_3
x1,x2,x3最多只能有2个,因此添加
y
1
+
y
2
+
y
3
≤
2
y_1+y_2+y_3le 2
y1+y2+y3≤2的约束。
然后是约束2,要求两座工厂二选一,因此添加Either-or变量
y
4
y_4
y4,最终模型为: