冒泡排序和选择排序
目录
一、冒泡排序
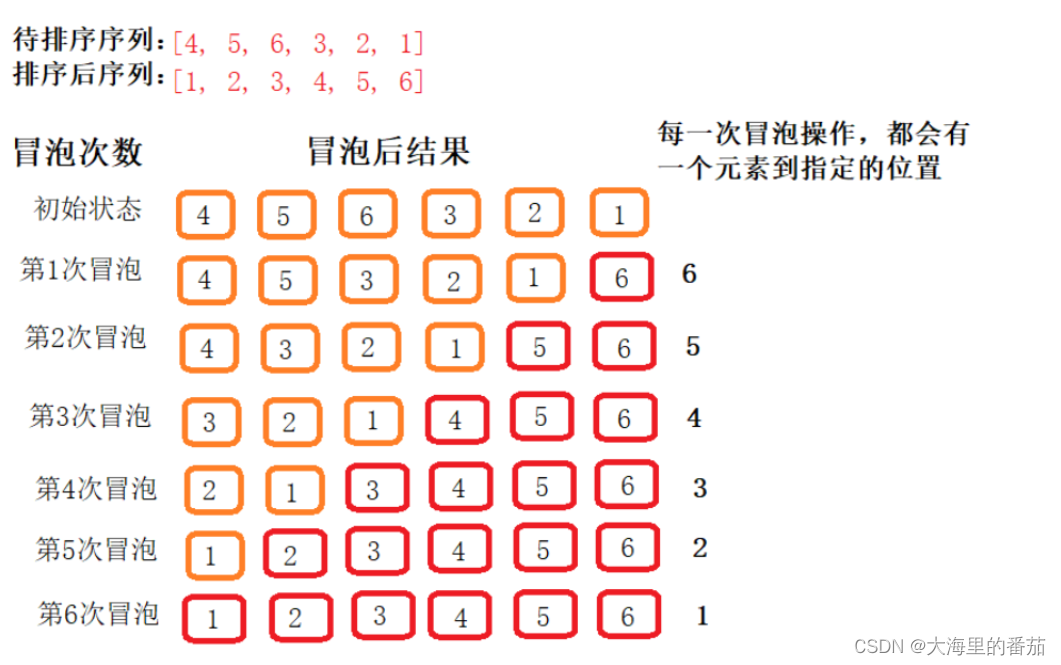
1.冒泡排序的原理
1.从尾部开始比较相邻的两个元素,如果尾部的元素比前面的大,就交换两个元素的位置。这种方法是排升序的,想排降序的话,一旦尾部的元素比前面的小就交换即可
比方说,我有一个数组,里面存放的是9 6 3,这三个数字,我的尾部是下标为0的数,也就是9,往下走遇到了6,9比6大,所以交换,数组就会变为6 9 3
2.往前对每个相邻的元素都做这样的比较和交换,未排序中最大(最小)的那个数就会被排到未排序的数的最后
2.实现冒泡排序
1.交换函数
通过原理的讲解不难看出,冒泡排序要实现多次的交换,因此我们可以写一个简单的交换函数
void Swap(int* x, int* y)
{
int tmp = *x;
//创建中间变量储存x
*x = *y;
*y = tmp;
}2.单躺排序
void BobbleSort(int* arr, int n)
//传递数组和数组元素个数
{
int j = 0;
for (j = 0; j < n - 1; j++)
//j<n-1避免越界
{
if (arr[j] > arr[j + 1])
//不断地进行比较,一遇到大的就进行交换,会将最大的数移动到数组的最后
{
Swap(&arr[j + 1], &arr[j]);
}
}
}3.冒泡排序实现
一趟排好一个数,那么我们一共有n个数,那么循环次数就可以修改成n次
void BobbleSort(int*arr,int n)
//传递数组和数组元素个数
{
int i = 0;
int j = 0;
for (i = 0; i < n; i++)
//n次排序排n个数
{
for (j = 0; j < n - 1; j++)
//j<n-1避免越界
{
if (arr[j] > arr[j + 1])
//不断地进行比较,一遇到大的就进行交换,会将最大的数移动到数组的最后
{
Swap(&arr[j + 1], &arr[j]);
}
}
}
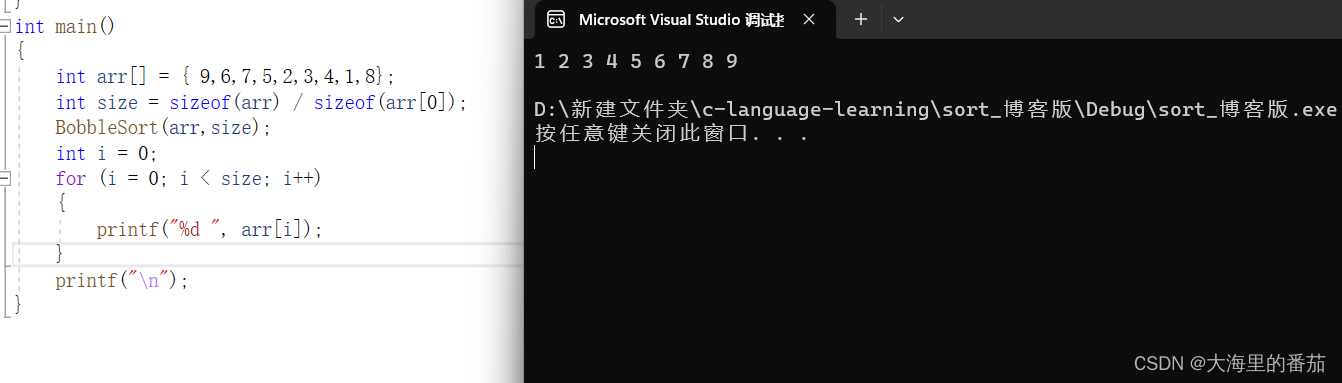
}4.测试
int main()
{
int arr[] = { 9,6,7,5,2,3,4,1,8};
int size = sizeof(arr) / sizeof(arr[0]);
BobbleSort(arr,size);
int i = 0;
for (i = 0; i < size; i++)
{
printf("%d ", arr[i]);
}
printf("n");
}
5.升级冒泡排序
1.我们可以看出,每次我们进行完一趟排序后,未排序中最大(最小)的那个数就会被排到未排序的数的最后,因此我们没有必要去和那些已经排好序的数作比较,所以我们可以把单躺循环判断语句改写成j<n-i-1,i代表已经排好序的数的个数,减去i就可以避免与这些数重复的比较。
2.如果数组已经有序我们还在比较显然就会浪费大量的时间 可以看出,如果数组无序的话,那个未排序中最大(最小)的那个数就会被排到未排序的数的最后,期间一定会出现交换,而如果有序的话就一定不会出现交换。
因此我们可以通过一个flaw变量来实现,每次进行新的一趟排序前,先将flaw变量初始化为1,一旦发生交换就令它为0,再在最外面根据flaw来判断是否发生了交换,如果发生了交换,那么数组依然无序,若是没有,则有序,结束函数
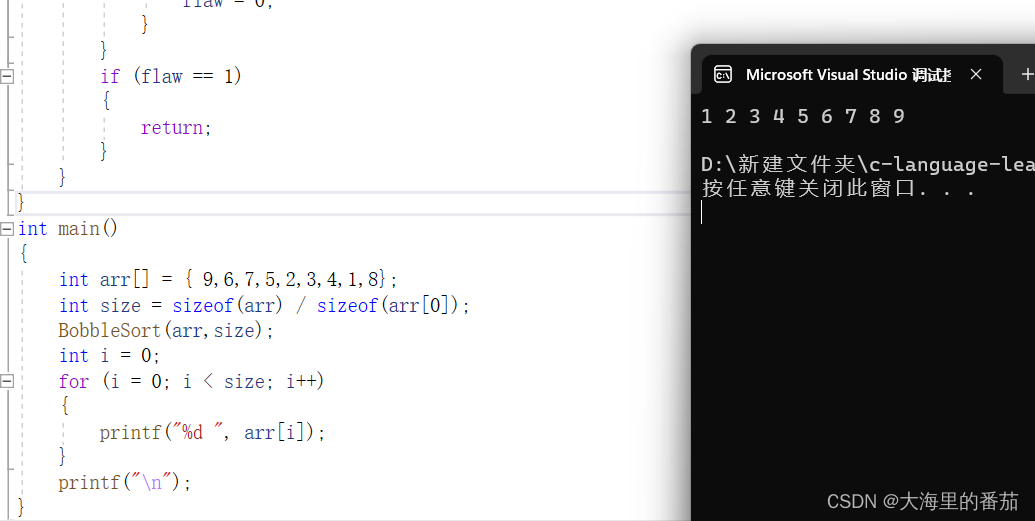
6.升级版代码
void BobbleSort(int*arr,int n)
//传递数组和数组元素个数
{
int i = 0;
int j = 0;
for (i = 0; i < n; i++)
//n次排序排n个数
{
int flaw = 1;
for (j = 0; j < n -i- 1; j++)
//j<n-1避免越界
{
if (arr[j] > arr[j + 1])
//不断地进行比较,一遇到大的就进行交换,会将最大的数移动到数组的最后
{
Swap(&arr[j + 1], &arr[j]);
flaw = 0;
}
}
if (flaw == 1)
{
return;
}
}
}7.升级版测试
二、选择排序
1.选择排序的原理
选择排序十分的简单粗暴,就是在数组中找到最大值和最小值,然后把它们放到对应的位置,如果你想排升序最大值放右边,最小值放左边,排降序相反即可。
2.实现选择排序
1.单躺排序
第一趟排序我们找到最大值和最小值然后把它们放在对应的位置即可
void SelectSort(int*arr,int n)
{
int max = 0;
int min = 0;
//max和min均储存下标
int i = 0;
for (i = 0; i < n; i++)
{
if (arr[max] < arr[i])
{
max = i;
}
if (arr[min] > arr[i])
{
min = i;
}
}
Swap(&arr[0] = &arr[min]);
//将最小值放到最前面
Swap(&arr[n-1],&arr[max]);
//将最大值放到最后
}2.选择排序实现
思考要排几趟,可以看出,每次都会将最大和最小的排到对应的位置,那么,循环差不多就是for(j=0;j<n/2;j++); 但要不要带上等号呢。这个可以代入实例进行思考,比方说,一共有5个元素,你要给它进行两次排序即可,而5/2=2,j<2,进行2次循环,满足条件,一共有6个元素,要进行三次排序,6/2*3,j<3,进行3次循环,满足条件。奇偶数均检验,故无需带上等于号。
思考细节,每比较一次,我们需要比较的区间就会缩小。所以应将查找最大最小的循环修改成for(i=j;i<n-j;i++); 同理,max和min的下标也不能一直都是0,区间减小了,你却使用到区间之外的数,显然不对,max,min应初始化为j
void SelectSort(int* arr, int n)
{
int i = 0; int j = 0;
for (j = 0; j < n / 2; j++)
{
int max = j; int min = j;
//max和min均储存下标
for (i = j; i < n - j; i++)
{
if (arr[max] < arr[i])
{
max = i;
}
if (arr[min] > arr[i])
{
min = i;
}
}
Swap(&arr[j], &arr[min]);
//将最小值放到最前面
Swap(&arr[n - 1 - j], &arr[max]);
//将最大值放到最后
}
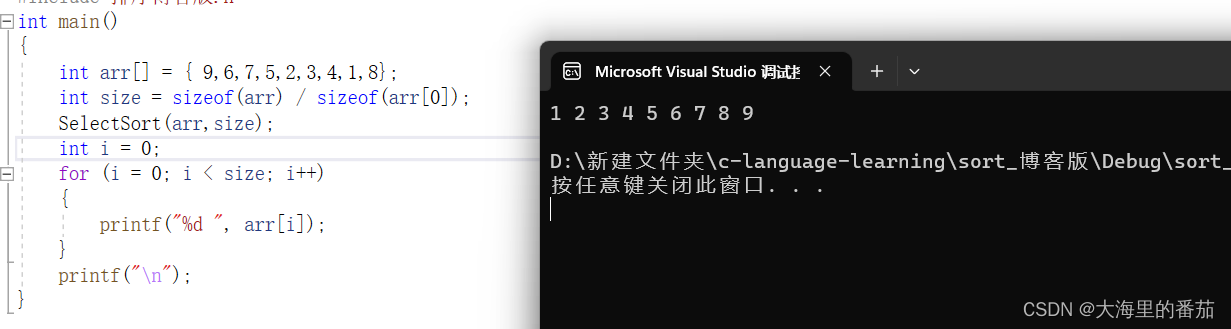
}3.测试
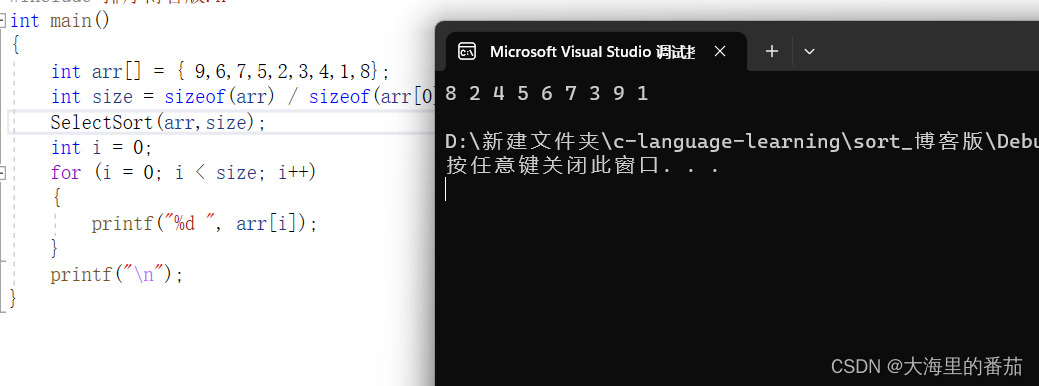 4.修改
4.修改
为什么会出错呢,仔细思考,你会发现,若是max和j相等的话,j先和min进行交换,那么此时的j就不再是最大值的下标了,自然会出错,因此,当max和j相等的时候,应该在交换之后使max更新为min,更新到真正最大值的下标。
void SelectSort(int* arr, int n)
{
int i = 0; int j = 0;
for (j = 0; j <n / 2; j++)
{
int max = j; int min = j;
//max和min均储存下标
for (i = j; i < n-j; i++)
{
if (arr[max] < arr[i])
{
max = i;
}
if (arr[min] > arr[i])
{
min = i;
}
}
Swap(&arr[j], &arr[min]);
//将最小值放到最前面
if (j == max)
//更新
{
max = min;
}
Swap(&arr[n - 1 - j], &arr[max]);
//将最大值放到最后
}
}5.测试
至此,冒泡排序和选择排序讲解完成,感谢各位友友的来访,祝各位友友前程似锦O(∩_∩)O