测距仪的似然域模型

似然域模型（Likelihood field model）克服了波束模型的局限性，能够在混乱小空间内，得到较为光滑的后验并大幅提高计算效率。

似然域模型是一种特设（ad hoc）算法，无合适的物理解释。

将障碍物检测的似然描述为地图坐标的函数，称为似然域。

模型建立

首先，模型将传感器扫描终点 z t z_t zt​映射至地图的全局坐标系（Map坐标系）。

假设机器人在时刻$t$的位姿 x t = [ X Y θ ] T x_t=begin{bmatrix}X&Y&thetaend{bmatrix}^T xt​=[X​Y​θ​]T，传感器相对于机器人坐标系（Footprint坐标系）的坐标为 [ X k , s e n s Y k , s e n s ] T begin{bmatrix}X_{k,sens}&Y_{k,sens}end{bmatrix}^T [Xk,sens​​Yk,sens​​]T，传感器波束相对机器人航向角的偏角为 θ k , s e n s theta_{k,sens} θk,sens​，传感器的测量终点为 z t k z_t^k ztk​，如图所示：

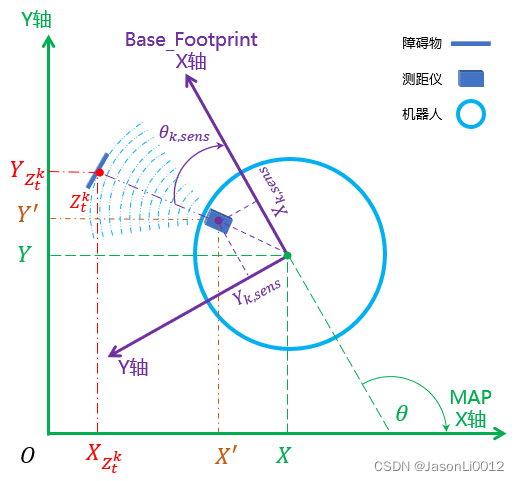
则通过2D平面坐标变换公式，可以得到传感器相对地图坐标系的坐标 [ X ′ Y ′ ] T begin{bmatrix}X^{'}&Y^{'}end{bmatrix}^T [X′​Y′​]T表达式
[ X ′ Y ′ ] = [ X Y ] + [ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ] [ X k , s e n s Y k , s e n s ] begin{bmatrix}X^{'}\Y^{'}end{bmatrix}=begin{bmatrix}X\Yend{bmatrix}+begin{bmatrix}costheta&-sintheta\sintheta&costhetaend{bmatrix}begin{bmatrix}X_{k,sens}\Y_{k,sens}end{bmatrix} [X′Y′​]=[XY​]+[cosθsinθ​−sinθcosθ​][Xk,sens​Yk,sens​​]
随后，考虑测量终点 z t k z_t^k ztk​在地图坐标系中的坐标 [ X z t k Y z t k ] T begin{bmatrix}X_{z_t^k}&Y_{z_t^k}end{bmatrix}^T [Xztk​​​Yztk​​​]T：
[ X z t k Y z t k ] = [ X ′ Y ′ ] + z t k [ cos ⁡ ( θ + θ k , s e n s ) sin ⁡ ( θ + θ k , s e n s ) ] begin{bmatrix}X_{z_t^k}\Y_{z_t^k}end{bmatrix}=begin{bmatrix}X^{'}\Y^{'}end{bmatrix}+z_t^kbegin{bmatrix}cos(theta+theta_{k,sens})\sin(theta+theta_{k,sens})end{bmatrix} [Xztk​​Yztk​​​]=[X′Y′​]+ztk​[cos(θ+θk,sens​)sin(θ+θk,sens​)​]
带入传感器坐标，可以得到：
[ X z t k Y z t k ] = [ X Y ] + [ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ] [ X k , s e n s Y k , s e n s ] + z t k [ cos ⁡ ( θ + θ k , s e n s ) sin ⁡ ( θ + θ k , s e n s ) ] begin{bmatrix}X_{z_t^k}\Y_{z_t^k}end{bmatrix}=begin{bmatrix}X\Yend{bmatrix}+begin{bmatrix}costheta&-sintheta\sintheta&costhetaend{bmatrix}begin{bmatrix}X_{k,sens}\Y_{k,sens}end{bmatrix}+z_t^kbegin{bmatrix}cos(theta+theta_{k,sens})\sin(theta+theta_{k,sens})end{bmatrix} [Xztk​​Yztk​​​]=[XY​]+[cosθsinθ​−sinθcosθ​][Xk,sens​Yk,sens​​]+ztk​[cos(θ+θk,sens​)sin(θ+θk,sens​)​]
需注意，当测距仪传回的测量值 z t k = z m a x z_t^k=z_{max} ztk​=zmax​时，表明存在异常噪声，该坐标在物理世界无意义，似然域模型将丢弃该读数。同波束模型一样，似然域模型考虑了三种噪声模型：

噪声一：测量噪声模型

对于测量过程中引起的噪声采用高斯分布进行建模，设在地图环境$m$中与测量坐标 [ X z t k Y z t k ] T begin{bmatrix}X_{z_t^k}&Y_{z_t^k}end{bmatrix}^T [Xztk​​​Yztk​​​]T最近的障碍物之间的欧氏距离为$dist$，则测量噪声可建模为均值为0，方差为 σ h i t 2 sigma_{hit}^2 σhit2​的高斯分布：
p h i t ( z t k ∣ x t , m ) = ε σ h i t ( d i s t ) p_{hit}(z_t^k|x_t,m)=varepsilon_{sigma_{hit}}(dist) phit​(ztk​∣xt​,m)=εσhit​​(dist)
式中，标准差 σ h i t sigma_{hit} σhit​为模型的固有参数。

如下左图，机器人在包含三个障碍物（灰色）的地图环境下进行测量，得到的测量点高斯似然如右图所示，图中越黑的地方存在障碍物的可能性越小；虚线表示传感器轴方向：

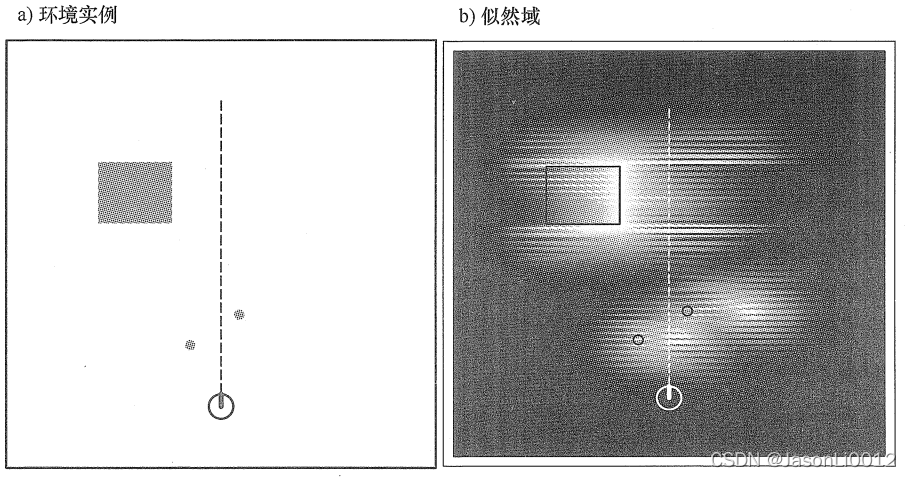
概率密度 p h i t p_{hit} phit​可由传感器轴正交归一化的似然域得到，如下所示为概率 p h i t ( z t k ) p_{hit}(z_t^k) phit​(ztk​)的曲线。该曲线表明传感器测量到三个障碍物对应曲线上 o 1 、 o 2 、 o 3 o_1、o_2、o_3 o1​、o2​、o3​所在位置。

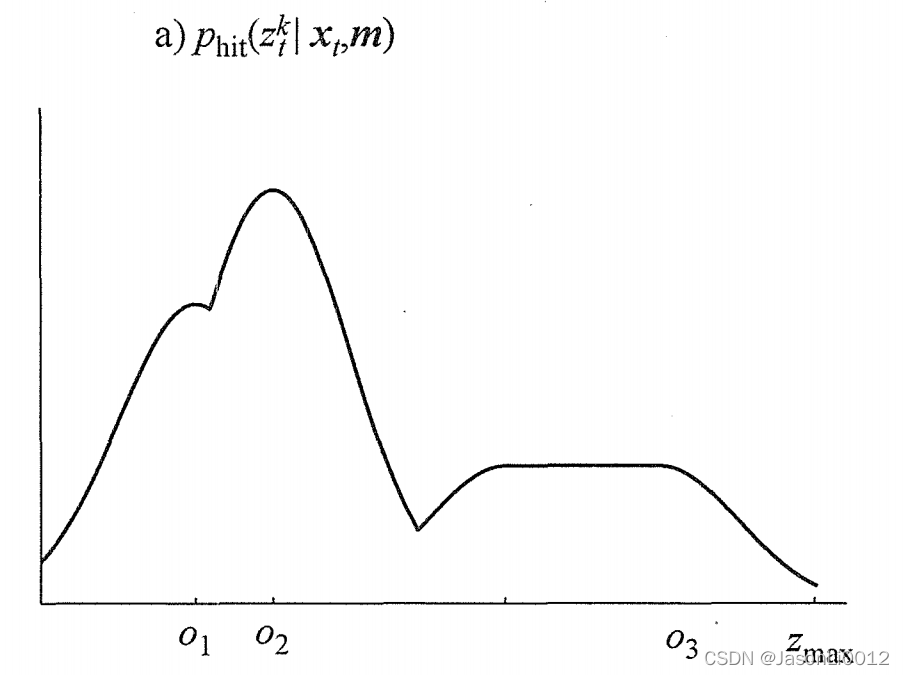
噪声二：失败噪声模型

当传感器返回 z t k = z m a x z_t^k=z_{max} ztk​=zmax​时，认为传感器测量失败，返回最大量程值 z m a x z_{max} zmax​。假定此时具有非常大的似然，则可用点群 p m a x p_{max} pmax​进行建模：
p m a x ( z t k ∣ x t , m ) = I ( z = z m a x ) = { 1 z = z m a x 0 其 他 p_{max}(z_t^k|x_t,m)=I(z=z_{max})=begin{cases}1quad&z=z_{max}\0quad&其他end{cases} pmax​(ztk​∣xt​,m)=I(z=zmax​)={10​z=zmax​其他​

噪声三：随机噪声模型

由于传感器在测量过程中，可能会出现无法解释的噪声现象，用均匀分布 p r a n d p_{rand} prand​对其进行建模：
p r a n d ( z t k ∣ x t , m ) = { 1 z m a x 0 ≤ z t k < z m a x 0 其 他 p_{rand}(z_t^k|x_t,m)=begin{cases}frac{1}{z_{max}}quad&0le z_t^k<z_{max}\ 0quad&其他end{cases} prand​(ztk​∣xt​,m)={zmax​1​0​0≤ztk​<zmax​其他​

似然域模型

由此，同波束模型一样，采用混合参数混合三种噪声，得到似然域模型如图所示：

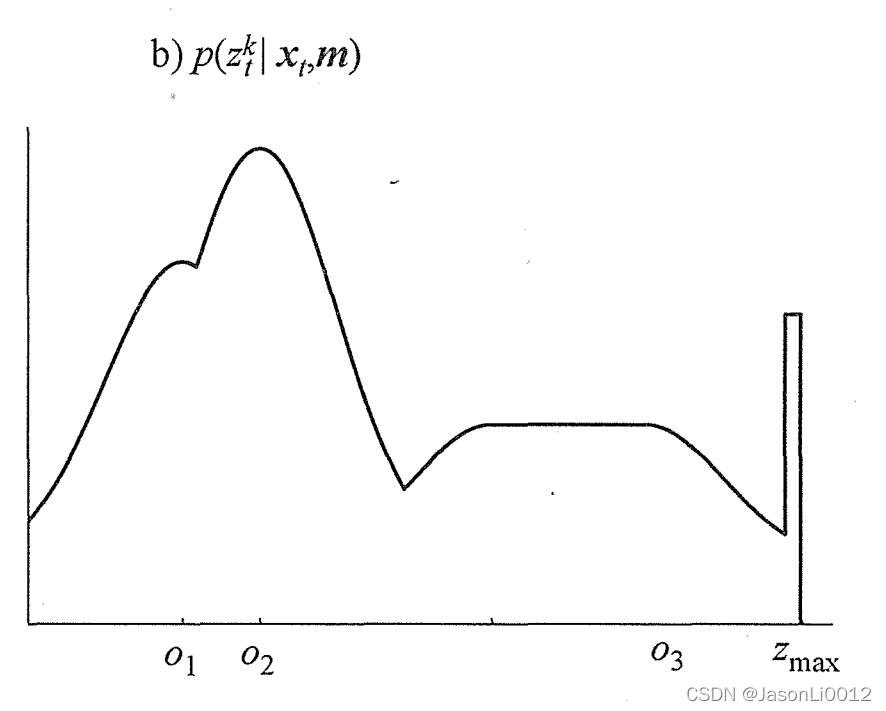
其表达式如下：
p ( z t k ∣ x t , m ) = [ z h i t z m a x z r a n d ] T ⋅ [ p h i t ( z t k ∣ x t , m ) p m a x ( z t k ∣ x t , m ) p r a n d ( z t k ∣ x t , m ) ] p(z_t^k|x_t,m)=begin{bmatrix}z_{hit}\z_{max}\z_{rand}end{bmatrix}^Tcdotbegin{bmatrix}p_{hit}(z_t^k|x_t,m)\p_{max}(z_t^k|x_t,m)\p_{rand}(z_t^k|x_t,m)\end{bmatrix} p(ztk​∣xt​,m)=⎣⎡​zhit​zmax​zrand​​⎦⎤​T⋅⎣⎡​phit​(ztk​∣xt​,m)pmax​(ztk​∣xt​,m)prand​(ztk​∣xt​,m)​⎦⎤​
式中，混合权数 z h i t 、 z m a x 、 z r a n d z_{hit}、z_{max}、z_{rand} zhit​、zmax​、zrand​和为1：
z h i t + z m a x + z r a n d = 1 z_{hit}+z_{max}+z_{rand}=1 zhit​+zmax​+zrand​=1

模型算法

系统输入： 完整的一组测量数据 z t z_t zt​、机器人位姿 x t x_t xt​、地图信息$m$

系统输出： 测量数据的可能性$q$
A l g o r i t h m l i k e l i h o o d _ f i e l d _ r a n g e _ f i n d e r _ m o d e l ( z t , x t , m ) : 1 : q = 1 2 : f o r a l l k d o 3 : i f z t k ≠ z m a x 4 : X z t k = X + X k , s e n s cos ⁡ θ − Y k , s n e s sin ⁡ θ + z t k cos ⁡ ( θ + θ k , s e n s ) 5 : Y z t k = Y + Y k , s e n s cos ⁡ θ + X k , s n e s sin ⁡ θ + z t k sin ⁡ ( θ + θ k , s e n s ) 6 : d i s t = min ⁡ X d , Y d { ( X z t k − X d ) 2 + ( Y z t k − Y d ) 2 ∣ ⟨ X d , Y d ⟩ o c c u p i e d i n m } 7 : q = q ⋅ ( z h i t ⋅ p r o b ( d i s t , σ h i t ) + z r a n d z m a x ) 8 : r e t u r n q begin{aligned} &Algorithmquad likelihood_field_range_finder_model(z_t,x_t,m):\ 1:&qquad q=1 \ 2:&qquad forenspace allenspace kenspace do \ 3:&qquadqquad if z_t^k neq z_{max}\ 4:&qquadqquadqquad X_{z_t^k}=X+X_{k,sens}costheta-Y_{k,snes}sintheta+z_t^kcos(theta+theta_{k,sens})\ 5:&qquadqquadqquad Y_{z_t^k}=Y+Y_{k,sens}costheta+ X_{k,snes}sintheta+z_t^ksin(theta+theta_{k,sens})\ 6:&qquadqquadqquad dist=min_{X_d,Y_d}Biggl{sqrt{(X_{z_t^k}-X_d)^2+(Y_{z_t^k}-Y_d)^2}Biggvert langle X_d,Y_drangleenspace occupiedenspace inenspace mBiggr}\ 7:&qquadqquadqquad q=qcdot Bigl(z_{hit}cdot prob(dist,sigma_{hit})+frac{z_{rand}}{z_{max}}Bigr)\ 8:&qquad returnquad q end{aligned} 1:2:3:4:5:6:7:8:​Algorithmlikelihood_field_range_finder_model(zt​,xt​,m):q=1forallkdoifztk​​=zmax​Xztk​​=X+Xk,sens​cosθ−Yk,snes​sinθ+ztk​cos(θ+θk,sens​)Yztk​​=Y+Yk,sens​cosθ+Xk,snes​sinθ+ztk​sin(θ+θk,sens​)dist=Xd​,Yd​min​{(Xztk​​−Xd​)2+(Yztk​​−Yd​)2 ​∣∣∣∣∣​⟨Xd​,Yd​⟩occupiedinm}q=q⋅(zhit​⋅prob(dist,σhit​)+zmax​zrand​​)returnq​
第一行，定义变量$q$存储整组数据 z t z_t zt​的概率

第二行，循环检测组内每个测量值 z t k z_t^k ztk​

第三行，判断是否为最大值，并抛弃最大输出

第四行~第五行，计算测量点在地图坐标系上的坐标值

第六行，计算地图信息上距离该测量点最近的障碍物的欧氏距离

第七行，混合高斯分布与均匀分布的噪声模型

最终，返回整组数据的准确性，模型的内参 Θ = { z h i t , z m a x , z r a n d , σ h i t } Theta={z_{hit},z_{max},z_{rand},sigma_{hit}} Θ={zhit​,zmax​,zrand​,σhit​}可用极大似然估计进行标定。

似然域模型的优缺点

欧氏距离的光滑性，致使机器人位姿 x t x_t xt​的微小改动将仅对分布结果 p ( z t k ∣ x t , m ) p(z_t^k|x_t,m) p(ztk​∣xt​,m)存在较小的影响，模型具有光滑性；

同时，模型的与计算采用二维空间代替了波束模型中的三维空间，降低了计算量。

与此同时，似然域模型存在如下缺点：

• 未考虑环境异常噪声 p s h o r t p_{short} pshort​，由此不能对人或动态清晰建模
• 射线投影被近邻函数代替，不能确定抵达某点路径是否被障碍物拦截
• 未考虑地图不确定性，不能处理地图上未知高度或未探测区域。

针对上述缺点，可将地图占用值扩展分为三类：占用、闲置、未知。当测量位置 z t k z_t^k ztk​处于地图未知区域时，假定其概率用均匀分布建模： p ( z t k ∣ x t , m ) = 1 z m a x p(z_t^k|x_t,m)=frac{1}{z_{max}} p(ztk​∣xt​,m)=zmax​1​