单调栈(C/C++)
目录
1. 单调栈的定义
单调栈顾名思义,就是栈内的元素是单调的。根据栈内元素的单调性的不同,可以分为:
单调递增栈:栈内元素是单调递增的栈。
单调递减栈:栈内元素是单调递减的栈。
2. 单调栈的常见用途
单调栈的用途:给定一个序列,指定一个序列中的元素,求解该元素 左侧/右侧 第一个比自身 小/大的元素。
这便是单调栈的常见用途。下面结合具体的例子来理解单调栈哈!N
3. 案例分析
原题链接:
496. 下一个更大元素 I - 力扣(LeetCode)
https://leetcode.cn/problems/next-greater-element-i/
题目描述:
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
3.1 暴力解法
暴力解法的思路就比较简单了。我们先初始化一个数组 ret,用他的下标表示 nums2 中的每一个元素,对应下标的值表示右侧第一个比它大的元素。然后从后往前(从前向后也行的)遍历 nums2 数组中的元素,遍历每一个元素时向后找比该元素更大的数,如果找到则将对应的结果保存到 下标为遍历元素的位置处,如果没有找到的话就将 -1 保存到下标为遍历元素的位置处。

得到了 nums2 数组中每个元素的右边第一个比自身大的元素后,只需要遍历一次 nums1 数组,在 ret 数组中找到结果就行啦!!
假设 nums2 数组的大小为 N,在求 nums2 数组中的每一个元素右侧第一个比自身大的数时,时间复杂度是一个等差数列的求和,即 O(N*N) 。在遍历 nums1 数组时,因为 nums1 数组中的元素是nums2 数组中元素的子集,遍历 nums1 的时间复杂度为 O(N),所以总的时间复杂度为:O(N^2)。
int* nextGreaterElement(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize)
{
int ret[10010];
int j;
for(int i = nums2Size - 1; i>=0;i--)
{
for(j = i + 1; j < nums2Size; j++)
{
if(nums2[j] > nums2[i])
{
ret[nums2[i]] = nums2[j];
break;
}
}
if(j == nums2Size)
{
ret[nums2[i]] = -1;
}
}
*returnSize = nums1Size;
int* array = (int*)malloc(sizeof(int)*nums1Size);
for(int i = 0;i<nums1Size;i++)
{
array[i] = ret[nums1[i]];
}
return array;
}
3.2 单调栈
单调栈的应用思路和双指针算法大体思路是一致的。先分析暴力解法怎么做,然后分析具体题目,找到其中隐藏的性质,从而达到优化时间效率的目的。
emm怎么分析的就不说了,后面会总结的。经过分析该问题发现:在向右找比自身大的元素时,哪些下标更大的,但是值却更小的元素是不可能作为结果输出到 ret 数组的。

分析到这里我们就可以用单调栈(为啥呢?找的是右侧第一个比自身大的元素,第一这两个字很能说明问题)来解决问题了!!我们这里使用的是用数组模拟的栈哈!效率比STL更高一点。向右找比自身大元素时,需要从后往前遍历 nums2 数组。
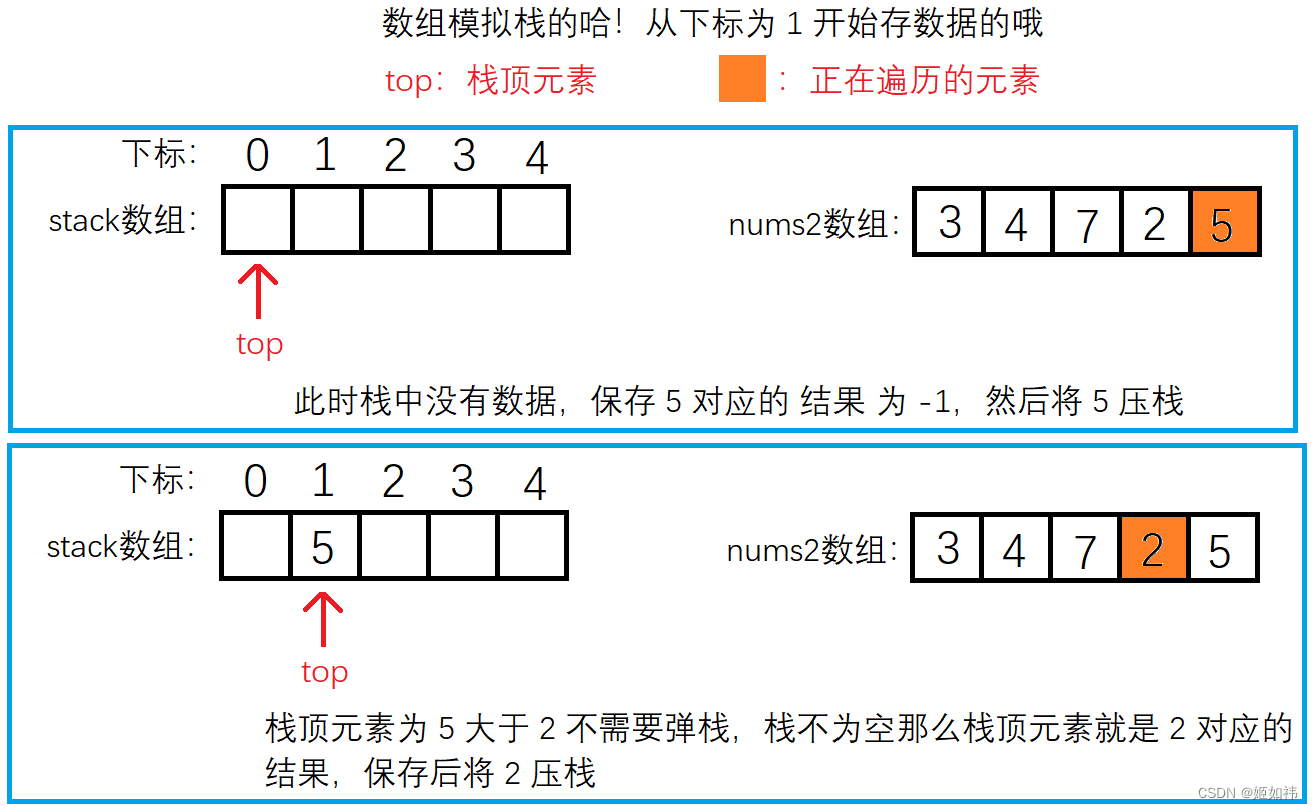
我们还是以上面的 3 4 7 2 5 来举例分析,开始遍历到 5 这个元素,此时栈为空,那就表明 5 这个元素右侧没有比自身大的元素(这里也能够说明为啥向右找需要从后往前遍历),将结果保存到 ret 数组。然后将 5 压入栈中。遍历到 2 时发现 2 小于栈顶的元素 5,表明 2 这个元素右侧第一个比自身大的元素是 5,将结果保存到 ret 数组中。遍历到 7 时,发现 7 大于栈顶的元素 2,这就是我们刚才说的,2 是不可能作为结果输出的,所以需要将栈顶的 2 弹出。弹出之后栈顶的元素就是 5 啦,同样 小于 7,但下标大于 7 的下标,需要再次弹出。此时我们发现栈里面已经没有元素了,说明 7 的右侧没有比自身大的元素 返回 -1。然后将 7 压入栈中。其他的元素就同理啦!
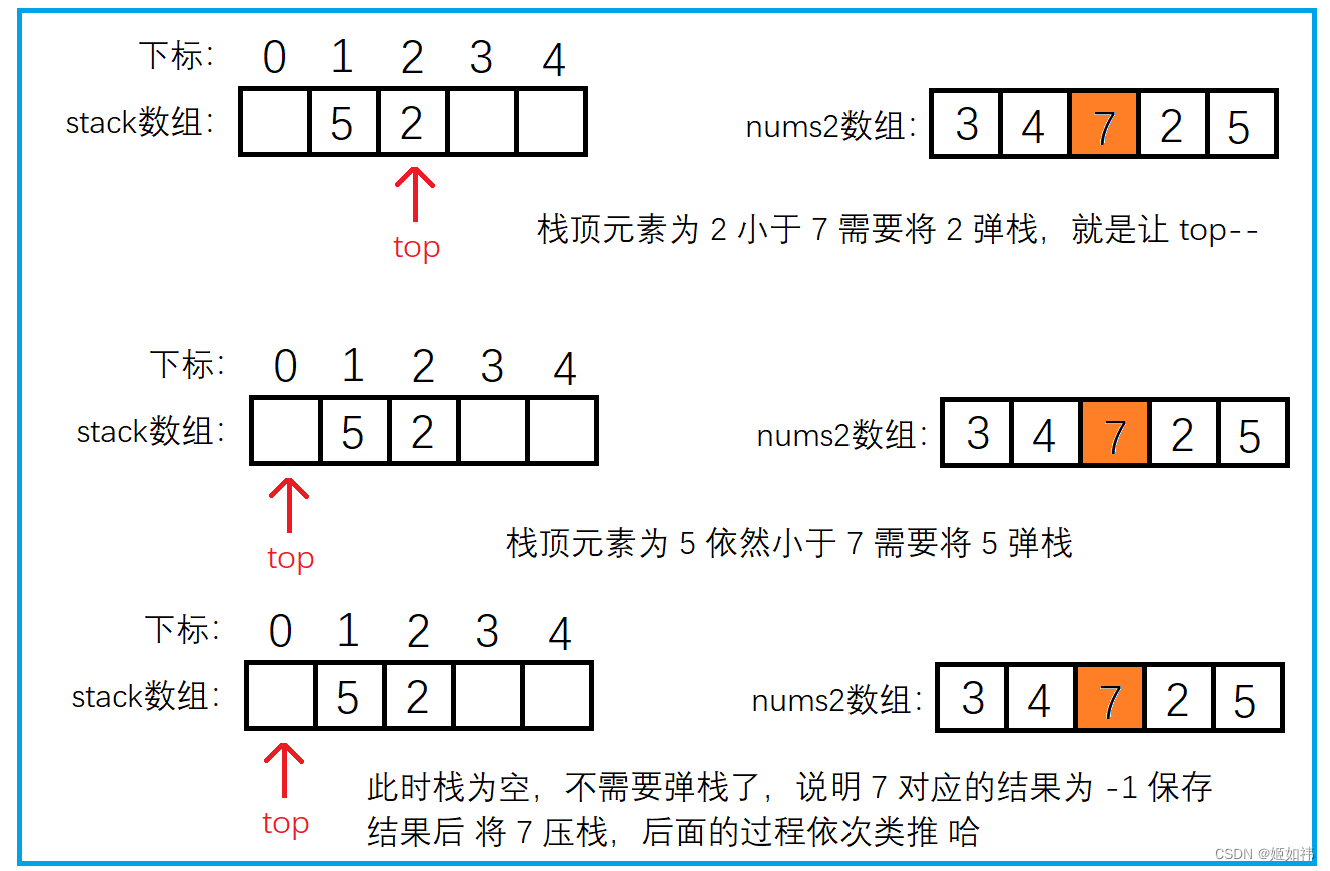
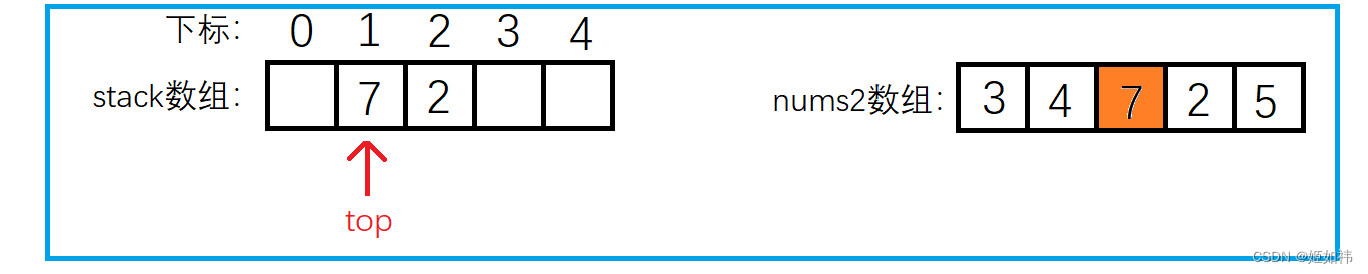
同样假设 nums2 数组的大小为 N,我们经过分析不难发现,nums2 中的元素 最多被 压栈一次,弹栈一次,所以找 nums2 数组中 右侧第一个 比自身大的数的时间复杂度为 O(N),遍历nums1数组输出结果时也是 O(N),因此总的时间复杂度就是 O(N)。
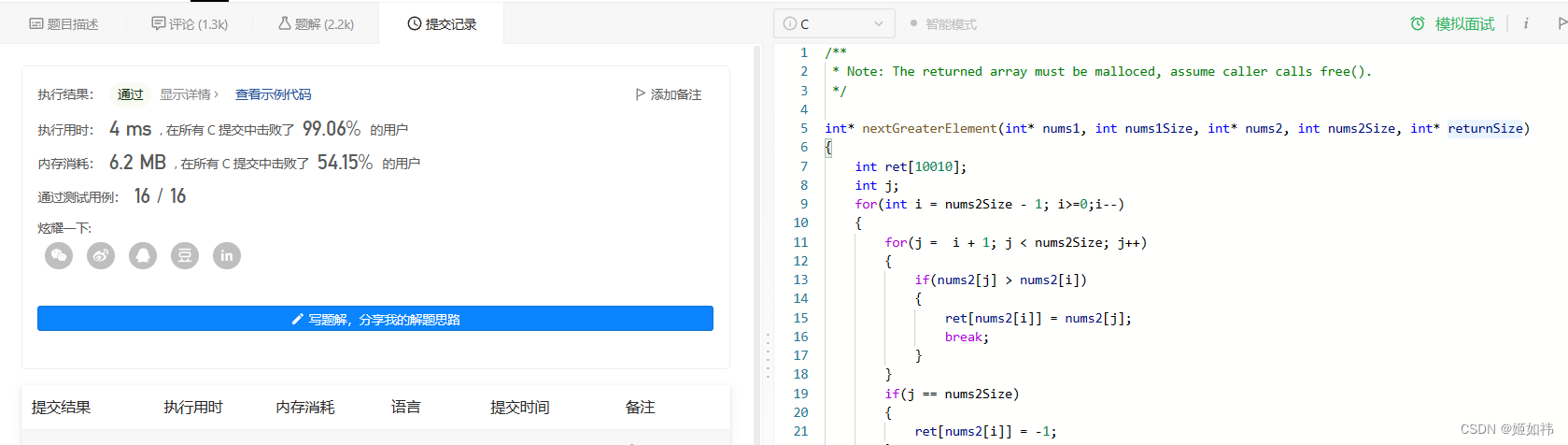
int* nextGreaterElement(int* nums1, int nums1Size, int* nums2, int nums2Size, int* returnSize){
int stack[nums2Size + 1], top = 0;
int ret[10010];
for(int i = nums2Size - 1; i >= 0; i--)
{
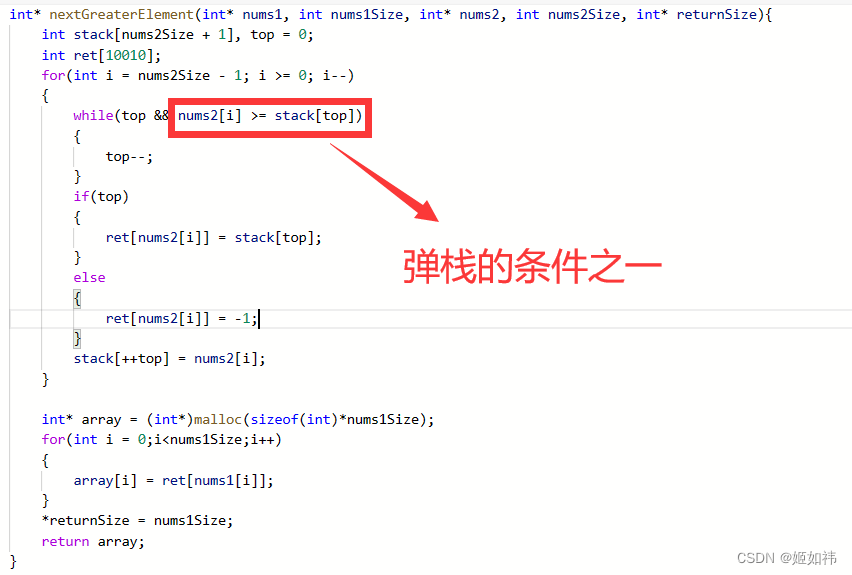
while(top && nums2[i] >= stack[top])
{
top--;
}
if(top)
{
ret[nums2[i]] = stack[top];
}
else
{
ret[nums2[i]] = -1;
}
stack[++top] = nums2[i];
}
int* array = (int*)malloc(sizeof(int)*nums1Size);
for(int i = 0;i<nums1Size;i++)
{
array[i] = ret[nums1[i]];
}
*returnSize = nums1Size;
return array;
}
4. 单调栈总结
单调栈的常见用途就是这个啦!显然是有四种情况的:
1:向左找第一个比自身大的数。
2:向左找第一个比自身小的数。
3:向右找第一个比自身大的数。
4:向右找第一个比自身小的数。
通过以上的解题我们可能会有以下问题:
1:从前往后遍历还是从后往前遍历?
答:向右找数从后往前遍历,向左找数从前往后遍历。
2:弹栈的条件之一是大于等于还是小于等于?
答:找比自身大的数弹栈条件之一是:正在遍历的元素大于等于栈顶元素。
找比自身小的数弹栈条件之一是:正在遍历的元素小于等于栈顶元素。