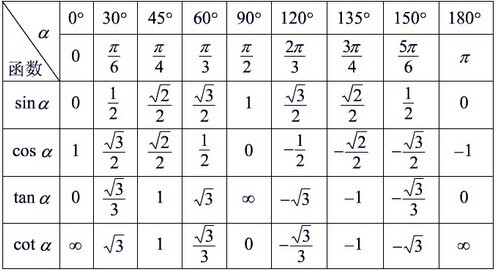
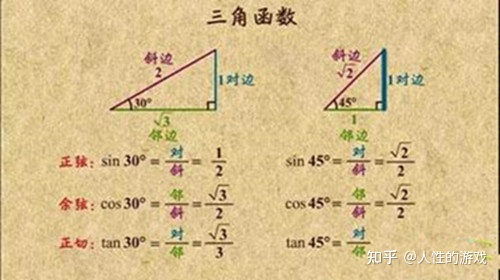
torch.atan2函数详细解答

先看看arctan

arctan实际上是用来计算点(x，y)组成的向量，与x轴的弧度的，是tan的反函数，推导如下，α为弧度

​

​

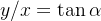
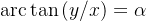
 y=arctan(x)其图像如下 y为弧度，x为任意值，这里不是指上面的坐标x，y

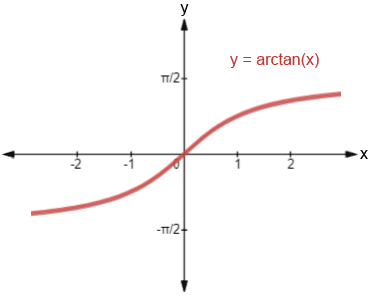
但这种弧度计算方式是有缺陷的，比如

我想区分如下图A、B两点的弧度，如果AB弧度都是

​

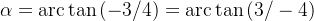
那么就无法区分开了，也就是虽然x,y有确定的唯一弧度，但同一个弧度会有两个刚好相反的向量指向，比如图中从原点到A和B的两条向量，不能唯一表示一个方向，这也就是atan2解决的东西 

​

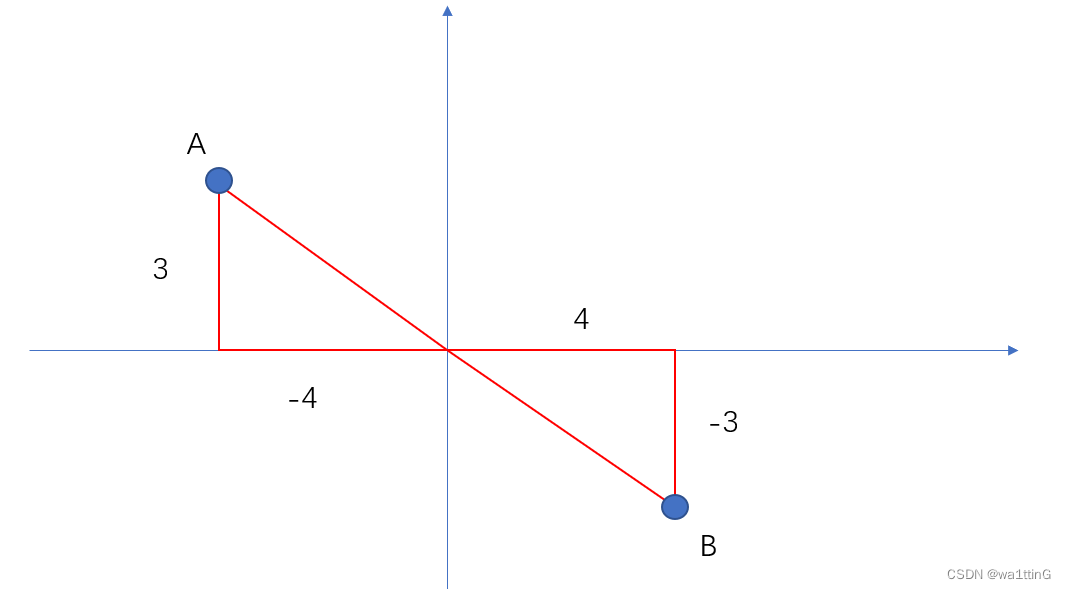
atan2

作用：计算一组点计算点(x，y)组成的向量的弧度，该弧度是与x轴正方向的弧度（这是与传统arctan的唯一区别）

 torch.atan2(input, other, *, out=None) → Tensor

• input (Tensor) – the first input tensor 是分子，也就是点y的坐标集合

• other (Tensor) – the second input tensor 是分母，也就是点x的坐标集合，otrher这里填入什么轴的值，就以什么轴的为正方向的夹角的弧度，在二维时other=x，就是该点与x轴正方向的弧度，在三维时other=z，就是该点与z轴正方向的弧度

在三角函数中，atan2是反正切函数的一个变种，有两个变数，主要是提供给计算机编程语言一个简便的弧度计算方式，其定义为：

​

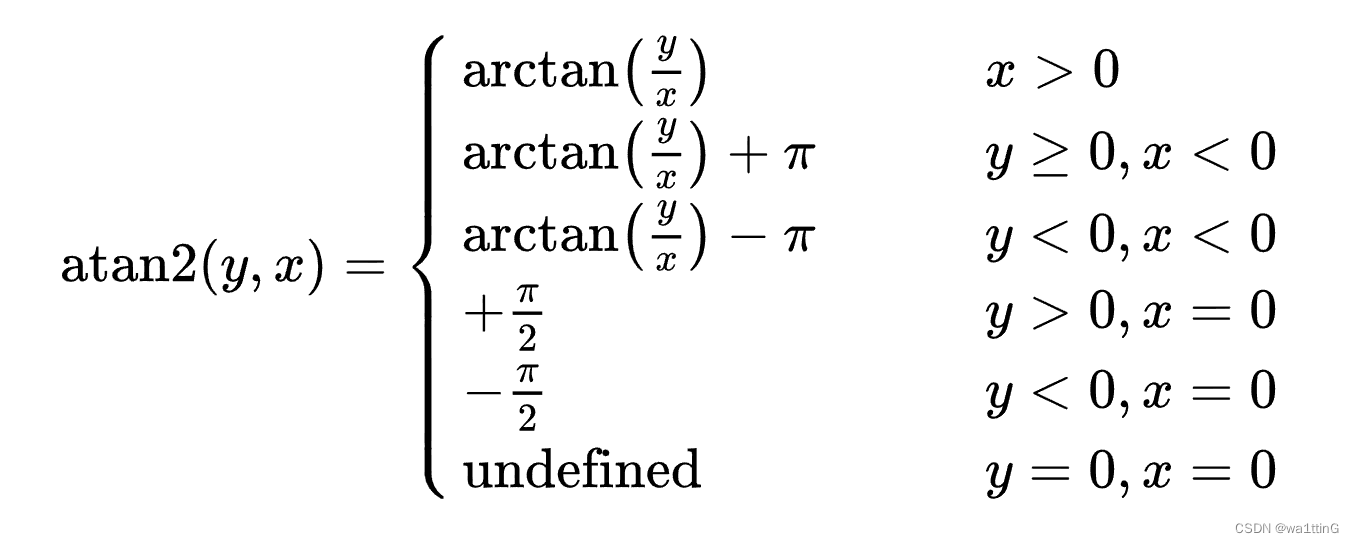
此时的atan2函数的图像如下，y为弧度，x为任意值

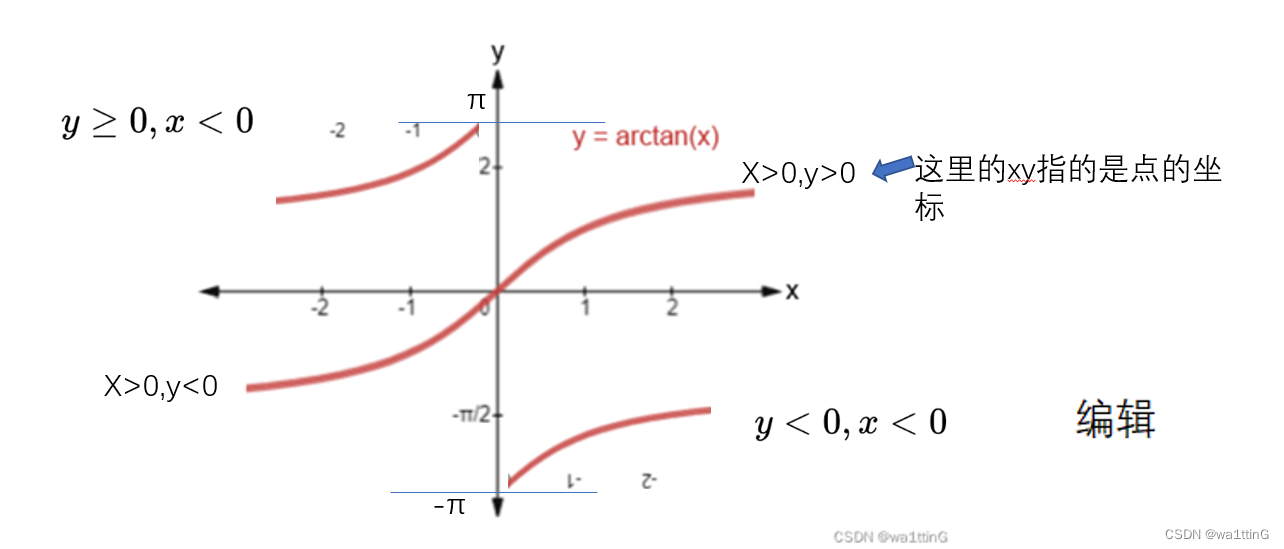
此时指定弧度有了唯一的象限，同一个弧度不会再出现有两条相反方向向量的情况了。

 此时A点的弧度=B的弧度+π，二者的弧度不再相等了，此时弧度相同，因为计算的是与x轴正半轴的弧度，也就是此时确定弧度可以唯一确定一个向量。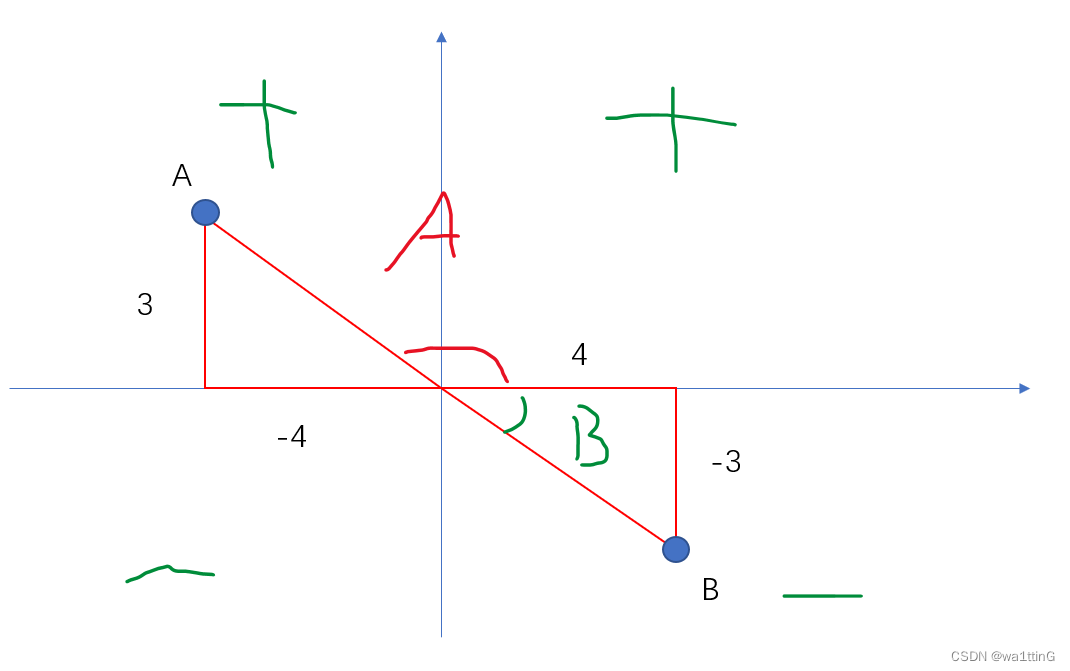

 torch.atan2的用法和结果验证

import torch
import numpy as np
from math import pi
x= torch.tensor([1,2,1])
y= torch.tensor([0,pi,2])

result=torch.atan2(y,x)
print(result)

print(np.arctan(pi/2))

tensor([0.0000, 1.0039, 1.1071])
1.0038848218538872

y为input，x为other，arctan(y[0]/x[0])，0=arctan(0/1)

1.0039=arctan(pi/2)

 torch.atan2对于三维空间的使用

在sphere former中，作者使用了如下的网络结构，将xyz转换为(θ，β，radius)的形式，该形式可以唯一地表示一个点。

def cart2sphere(xyz):
    '''
    将xyz坐标转化为弧度坐标[theta, beta, r]
    Args:
        xyz:

    Returns:[theta, beta, r]，y与x轴的夹角theta，xy平面上的投影与

    '''
    x, y, z = xyz[:, 0], xyz[:, 1], xyz[:, 2]
    #計算該點於x軸正方向的弧度
    theta = (torch.atan2(y, x) + np.pi) * 180 / np.pi #將弧度值都變爲正值，最後變成角度值，theta 0-360。
    # 計算該點於z軸正方向的弧度
    beta = torch.atan2(torch.sqrt(x**2 + y**2), z) * 180 / np.pi #轉換結果爲角度，第一项永远为正数,也就是y大于0，因此结果y永远为正数 0~180,
    r = torch.sqrt(x**2 + y**2 + z**2)#r是半徑
    return torch.stack([theta, beta, r], -1) 

为什么该形式可以唯一表示一个点呢？

首先，(x,y,z)可以唯一确定1组(θ，β，radius)，通过上述代码，(x,y,z)可以得到唯一的一组确定的解。

我们进行分析是否有可能一个(θ，β，radius)可以映射到两个讲过0点的向量（x,y，z）上,

点(x,y,z)可以看做是三个向量x，y，z的合成

theta = (torch.atan2(y, x) + np.pi) * 180 / np.pi

 torch.atan2(y, x)就是上面提到的，一个θ有确定的一个x，y向量。

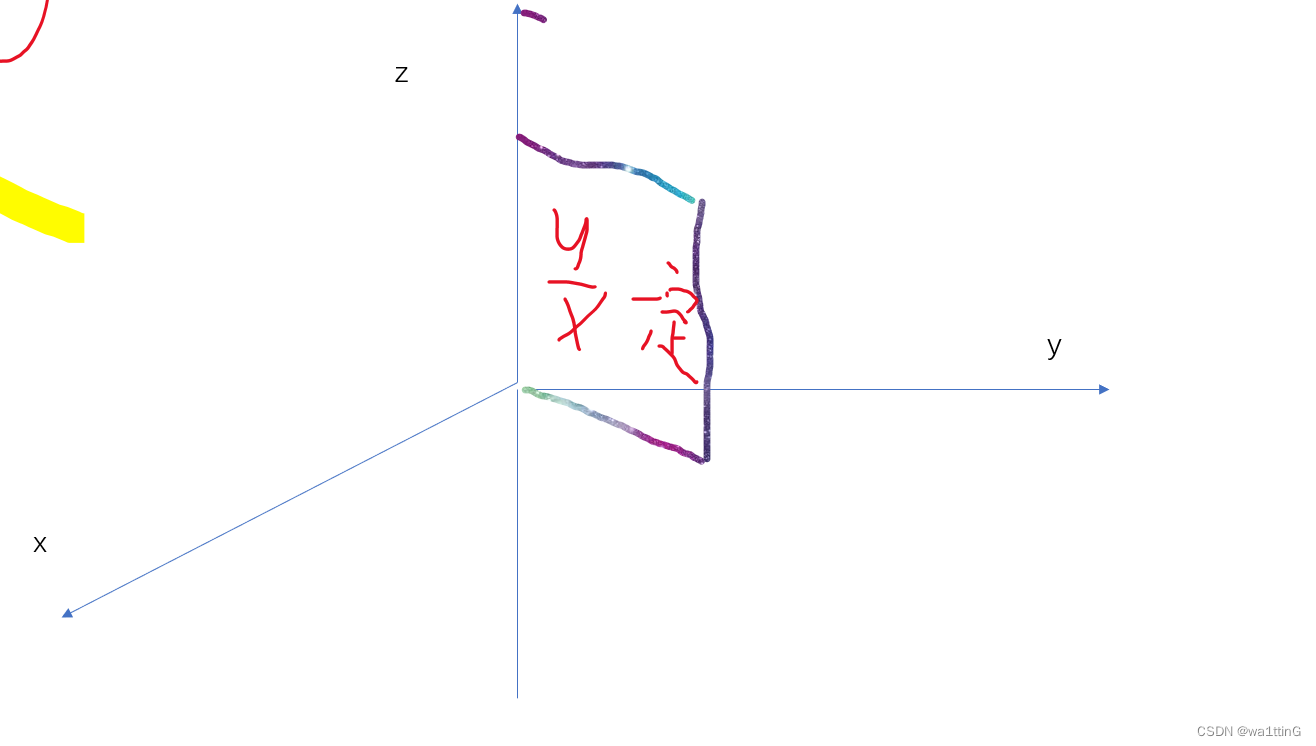
beta = torch.atan2(torch.sqrt(x**2 + y**2), z) 

该行代码可以计算该点torch.sqrt(x**2 + y**2)（永远在第一、二象限）和z组成的向量与z轴正方向的弧度，因为z在第二个参数位置上，所以是以z轴为正方向。

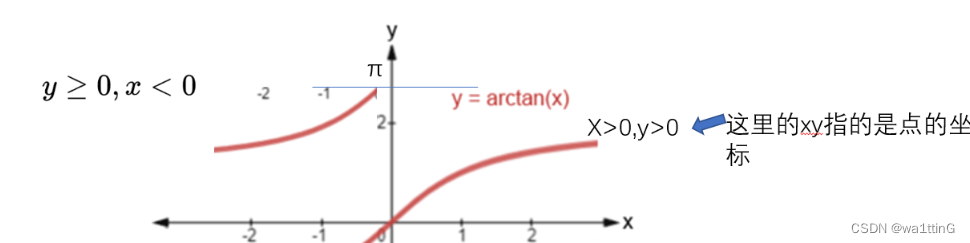
 也就是x轴现在变为torch.sqrt(x**2 + y**2)/z，y轴变为β，torch.sqrt(x**2 + y**2)永远大于0（图上就是y>0），也就是只有其大于0的部分，对应了这两条曲线，也就是β确定，torch.sqrt(x**2 + y**2)/z唯一确定，如下图，由于torch.sqrt(x**2 + y**2)恒大于0，并不会出现两条完全相反的向量，因此不会出现1个弧度对应两个向量的问题。

 再在该平面上画半径，只有唯一的交点。

也就是θ确定x、y平面上的方向，β确定z，（x+y）平面的方向，半径确定该x，y,z方向上的唯一点。

附：角度与弧度的关系

弧度角度转换

2*pi=2*pi*180°/pi=2*180°=360°

arctan是tan的反函数，而不是倒数的关系