PCA主成分分析（降维）

主成分分析的作用是降维。当数据量有多个维度时，有些维度对于数据的贡献大，有些维度对数据的贡献小。通过主成分分析，找到重要的维度，能大大减少计算量。

PCA的中心思想：

一个中心：原始特征空间的重构。

两个基本点：最大投影方差，最小重构距离。

---------------------------------------------------------------------------------------------------------------------------------

最小重构距离通过下面的式子来构建。

重构前：(xn是去中心化的每个样本)

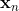$mathbf{x}_{n}=sum_{d=1}^{D} alpha_{n d} mathbf{u}_{d}=sum_{m=1}^{M} alpha_{n m} mathbf{u}_{m}+sum_{i=M+1}^{D} alpha_{n i} mathbf{u}_{i}$

$mathbf{x}_{n}$ 表示原始的点，能表示成d个向量（d个维度）的和。通过分解，它能够分解到两组向量上，PCA保留了一部分，舍弃了一部分，舍弃了 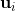$mathbf{u}_{i}$ 这部分，保留了 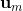$mathbf{u}_{m}$ 这部分。a是每个分解的向量u上的长度，相乘后求和就可以重构原样本。

重构后：

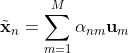
$tilde{mathbf{x}}_{n}=sum_{m=1}^{M} alpha_{n m} mathbf{u}_{m}$

重构的代价就是使重构前后的距离最小：（两个式子相减后剩下后面这部分）

$begin{aligned} J=frac{1}{N} sum_{n=1}^{N}left|mathbf{x}_{n}-tilde{mathbf{x}}_{n}right|^{2}=& frac{1}{N} sum_{n=1}^{N}left|sum_{i=M+1}^{D} alpha_{n i} mathbf{u}_{i}right|^{2}=frac{1}{N} sum_{n=1}^{N} sum_{i=M+1}^{D} alpha_{n i}^{2}=sum_{i=M+1}^{D} mathbf{ frac{1}{N}({u}_{i}^{T} x_{n})(x_{n}^{T}} mathbf{u}_{i})=sum_{i=M+1}^{D} mathbf{u}_{i}^{T} mathbf{S} mathbf{u}_{i} \ & text {where} mathbf{S}=frac{1}{N} sum_{n=1}^{N} mathbf{x}_{n} mathbf{x}_{n}^{T} quad text { (covariance matrix) } end{aligned}$

这里的S是协方差矩阵。

则损失函数为：

$J=sum_{i=M+1}^{D} mathbf{u}_{i}^{T} mathbf{S u}_{i}$

使用拉格朗日乘子约束优化，式子变成：

$J=sum_{i=M+1}^{D} mathbf{u}_{i}^{T} mathbf{S u}_{i}+lambdaleft(1-mathbf{u}_{i}^{T} mathbf{u}_{i}right)$

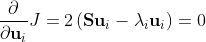
$frac{partial}{partial mathbf{u}_{i}} J=2left(mathbf{S} mathbf{u}_{i}-lambda_{i} mathbf{u}_{i}right)=0$

则：

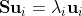
$mathbf{S} mathbf{u}_{i}=lambda_{i} mathbf{u}_{i}$

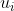$u_{i}$ 表示S的特征向量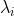， $lambda_{i}$ 表示特征值。

---------------------------------------------------------------------------------------------------------------------------------

则PCA的步骤为：

1.求平均值，去中心化

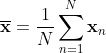
$overline{mathbf{x}}=frac{1}{N} sum_{n=1}^{N} mathbf{x}_{n}$

$mathbf{x}_{n}^{text {norm }}=mathbf{x}_{n}-overline{mathbf{x}}, quad forall n in{1, ldots, N}$

2.计算协方差矩阵

$mathbf{S}=frac{1}{N} sum_{n=1}^{N} mathbf{x}_{n}^{text {norm }}left[mathbf{x}_{n}^{text {norm }}right]^{T}$

3.特征分解

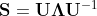
$mathbf{S}=mathbf{U} boldsymbol{Lambda} mathbf{U}^{-1}$

矩阵分解的过程就像下面这样子

$mathbf{S}=left[begin{array}{ccc}sigma_{11}^{2} & ldots & sigma_{1 M}^{2} \ vdots & ddots & vdots \ sigma_{M 1}^{2} & cdots & sigma_{M M}^{2}end{array}right]=mathbf{U} boldsymbol{Lambda} mathbf{U}^{T}=left[begin{array}{lll}mathbf{U}_{s} & mid & mathbf{U}_{mathbf{n}}end{array}right]left[begin{array}{c|c}boldsymbol{Lambda}_{s} & mathbf{0} \ hline mathbf{0} & boldsymbol{Lambda}_{n}end{array}right]left[begin{array}{c}mathbf{U}_{s}^{T} \ hline mathbf{U}_{mathbf{n}}{ }^{T}end{array}right]$

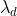4.用特征值 $lambda_{d}$ 对U的列进行排序

5.选择M个特征向量，形成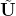

6.进行投影

$tilde{mathbf{x}}_{n}=tilde{mathbf{U}} tilde{mathbf{U}}^{T} mathbf{x}_{n}^{text {norm }}+overline{mathbf{x}}$

$J=sum_{i=M+1}^{D} lambda_{i}$