算法分析与设计编程题 贪心算法

活动安排问题

题目描述

解题代码

vector<bool> greedySelector(vector<vector<int>>& intervals) {
    int n = intervals.size();
    // 将活动区间按结束时间的从小到大排序
    auto cmp = [](vector<int>& interval1, vector<int>& interval2) {
        return interval1[1] < interval2[1];
    };
    sort(intervals.begin(), intervals.end(), cmp);
    vector<bool> res(n, false);
    // 结束时间最早的活动必定位于某个最优解之中
    int minStart = intervals[0][1];
    res[0] = true;
    for (int i = 1; i < n; ++i) {
        if (intervals[i][0] >= minStart) { // 将不重叠的活动加入最优解集
            res[i] = true;
            minStart = intervals[i][1];
        }
    }
    return res;
}

最优装载

题目描述

解题代码

vector<bool> optimisedLoading(vector<int>& weight, int c) {
	int n = weight.size();
	vector<bool> select(n, false);
    // 定义一个小顶优先队列，使得对于i，若其weight[i]最小，则排在队列的队头
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
	for (int i = 0; i < n; ++i) {
        // 构建二元组<重量,下标>并放入优先队列
		q.emplace(weight[i], i);
	}
	for (int i = 0; i < n; ++i) {
		auto [w, idx] = q.top(); // （C++17语法）取队头元素的w和对应下标
		q.pop();
		if (c < w) break; // 无法继续装载
		select[idx] = true; // 选择装载该货物
		c -= w; // 剩余载货量减少
	}
	return select;
}

哈夫曼编码

题目描述

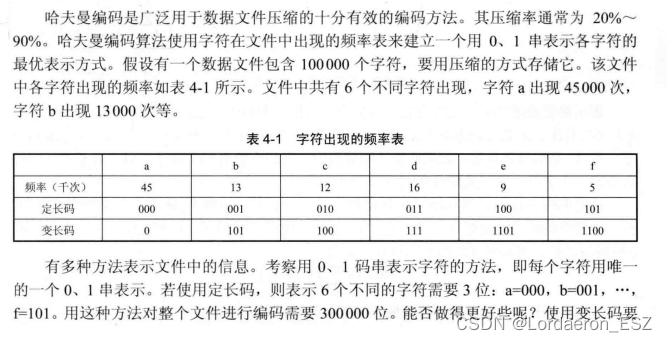
解题代码

struct HuffmanNode {
	int left, right; // 左右结点
	int parent; // 父结点
	int weight; // 权重
	char data; // 数据
	HuffmanNode(int left = -1, int right = -1, int parent = -1, int weight = 0, char data = '*')
		: left(left), right(right), parent(parent), weight(weight), data(data) {}
};

vector<HuffmanNode> createHuffmanTree(vector<int>& weight, vector<char>& data) {
	int n = weight.size();
	vector<HuffmanNode> huffmanTree(2 * n);
    // 定义一个小顶优先队列，使得对于i，若其weight[i]最小，则排在队列的队头
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
	for (int i = 0; i < n; ++i) { // 初始化哈夫曼树和优先队列
		huffmanTree[i].data = data[i];
		huffmanTree[i].weight = weight[i];
		q.emplace(weight[i], i);
	}
	for (int i = 0; i < n - 1; ++i) {
		auto [weight1, idx1] = q.top(); // 取权值最小结点
		q.pop();
		auto [weight2, idx2] = q.top(); // 取权值第二小结点
		q.pop();
        // 创建两结点的父结点，其下标为n+i
		huffmanTree[idx1].parent = n + i;
		huffmanTree[idx2].parent = n + i;
		// 初始化该父结点的相关信息
		huffmanTree[n + i].left = idx1;
		huffmanTree[n + i].right = idx2;
		huffmanTree[n + i].weight = weight1 + weight2;
        // 将该父结点的<权值,下标>加入优先队列，以便进行贪心选择
		q.emplace(weight1 + weight2, n + i);
	}
	return huffmanTree;
}

void printHuffmanCode(vector<HuffmanNode>& huffmanTree) {
	stack<int> s;
	for (int i = 0; i < huffmanTree.size() / 2; ++i) {
		int cur = i; // 当前结点下标
		int pre = huffmanTree[cur].parent; // 当前结点的父结点的下标
		while (pre != -1) {
			if (huffmanTree[pre].left == cur) {
				s.emplace(0); // 当前结点为其父结点的左孩子
			}
			else {
				s.emplace(1); // 当前结点为其父结点的右孩子
			}
            // 轮换下标
			cur = pre;
			pre = huffmanTree[cur].parent;
		}
        // 打印相应的哈夫曼编码
		cout << huffmanTree[i].data << " ";
		while (!s.empty()) {
			cout << s.top();
			s.pop();
		}
		cout << endl;
	}
}

单源最短路径

题目描述

解题代码

图的定义

struct MGraph {
	vector<char> vertices; // 顶点数组
	vector<vector<int>> edges; // 邻接矩阵
};

BellmanFord

此算法可适用于含有负权值边的图。

// G:图	start:源点	dist:最短路径
bool BellmanFord(MGraph& G, int start, vector<int>& dist) {
	int n = G.vertices.size();
	// 初始化最短路径
	dist.assign(n, INT32_MAX);
	for (int j = 0; j < n; ++j) {
		dist[j] = G.edges[start][j];
	}
	for (int t = 0; t < n - 1; ++t) { // 松弛次数t
		for (int i = 0; i < n; ++i) { // 边的起点i
			for (int j = 0; j < n; ++j) { // 边的终点j
				if (G.edges[i][j] != INT32_MAX && dist[i] != INT32_MAX
					&& dist[i] + G.edges[i][j] < dist[j]) {
					dist[j] = dist[i] + G.edges[i][j]; // 松弛操作
				}
			}
		}
	}
	for (int i = 0; i < n; ++i) {
		for (int j = 0; j < n; ++j) {
			// 若执行完算法后仍然存在非最短路径，则该图存在权值为负的环路，无最短路径
			if (G.edges[i][j] != INT32_MAX && dist[i] != INT32_MAX
				&& dist[i] + G.edges[i][j] < dist[j]) {
				return false;
			}
		}
	}
	return true;
}

Dijkstra

本算法仅适用于所有边的权值均为正的图。

// G:图	start:源点	dist:最短路径
void Dijkstra(MGraph& G, int start, vector<int>& dist) {
	int n = G.vertices.size();
	// 初始化最短路径
	dist.assign(n, INT32_MAX);
	vector<int> pre(n, -1); // 前驱数组
	vector<bool> visited(n, false); // 访问集，表示对应顶点最短路径是否已经找到
	visited[start] = true;
	// 小顶优先队列，元素为<dist[j],j>
	priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> q;
	// 初始化最短路径
	for (int j = 0; j < n; ++j) {
		dist[j] = G.edges[start][j];
		q.emplace(dist[j], j);
	}
	while (!q.empty()) {
		int i = q.top().second; // 贪心选择最近结点i
		q.pop();
		visited[i] = true; // 结点i最短路径已得到
		for (int j = 0; j < n; ++j) { // 利用结点i进行松弛操作
			if (visited[j]) continue; // 结点j已得到最短路径，无需松弛
			if (G.edges[i][j] != INT32_MAX && dist[i] != INT32_MAX
				&& dist[i] + G.edges[i][j] < dist[j]) {
				dist[j] = dist[i] + G.edges[i][j]; // 松弛操作
				pre[j] = i; // 更新前驱结点
				q.emplace(dist[j], j); // 加入优先队列
			}
		}
	}
	// 打印源点到各结点的最短路径
	stack<int> s;
	for (int i = 0; i < n; ++i) {
		if (i == start) continue;
		if (dist[i] == INT32_MAX) {
			cout << "inf" << ": " << G.vertices[start] << "->" << G.vertices[i] << endl;
		}
		else {
			cout << dist[i] << ": " << G.vertices[start] << "->";
			int x = pre[i];
			while (x != -1) {
				s.emplace(x);
				x = pre[x];
			}
			while (!s.empty()) {
				cout << G.vertices[s.top()] << "->";
				s.pop();
			}
			cout << G.vertices[i] << endl;
		}
	}
}

最小生成树

题目描述

解题代码

Kruskal

void Kruskal(MGraph& G) {
	int n = G.vertices.size();
    // 边集，元素为<权值weight，起点u，终点v>
	vector<tuple<int, int, int>> edges;
	for (int i = 0; i < n; ++i) {
		for (int j = i + 1; j < n; ++j) {
			if (G.edges[i][j] != INT32_MAX) {
                // 将边加入边集
				edges.emplace_back(G.edges[i][j], i, j);
			}
		}
	}
    // 对边集按权值大小进行升序排序
	sort(edges.begin(), edges.end());
    // 简单并查集，father[x]存放x的父结点
	vector<int> father(n);
    // 寻找x所在集合的父结点（所在连通分量编号）
	auto findFather = [&](int x) {
		int f = father[x];
		while (f != x) {
			x = f;
			f = father[x];
		}
		return f;
	};
	for (int i = 0; i < n; ++i) {
		father[i] = i; // 初始父结点为自身
	}
	int cnt = 0; // 已找到的边个数
	for (int i = 0; cnt <= n - 1 && i < edges.size(); ++i) {
		auto [weight, u, v] = edges[i];
		int fu = findFather(u);
		int fv = findFather(v);
		// 若u和v父结点相同（即u和v位于一个连通分量中），若选择加入边uv，则会导致回路
        if (fu != fv) { 
			cout << G.vertices[u] << " - " << G.vertices[v] << " : " << weight << endl;
			father[fu] = fv; // 两个连通分量合并为一个
			++cnt;
		}
	}
}

Prim

void Prim(MGraph& G) {
	int n = G.vertices.size();
    // minDist[i]表示结点i距离MST最近距离
	vector<int> minDist(n, INT32_MAX);
    // connected[i]表示在MST中与结点i相连的结点
	vector<int> connected(n, 0);
    // 表示结点i是否已加入MST
	vector<bool> visited(n, false);
	visited[0] = true;
	for (int j = 1; j < n; ++j) {
        // 初始化最近距离
		minDist[j] = G.edges[0][j];
	}
	for (int i = 1; i < n; ++i) {
        // 寻找距离MST的最近结点k
		int minVal = INT32_MAX, k = -1;
		for (int j = 1; j < n; ++j) {
			if (!visited[j] && minDist[j] < minVal) {
				minVal = minDist[j];
				k = j;
			}
		}
		if (k == -1) break;
        // 将结点k加入MST中
		visited[k] = true;
		cout << G.vertices[connected[k]] << " - " << G.vertices[k] << " : " << minVal << endl;
        // 更新minDist数组和connected数组
		for (int j = 1; j < n; ++j) {
			if (!visited[j] && G.edges[k][j] < minDist[j]) {
				minDist[j] = G.edges[k][j];
				connected[j] = k;
			}
		}
	}
}