Java【数据结构】二分查找
? 题目:
?在有序数组A中,查找目标值target
?如果找到返回索引
?如果找不到返回-1
| 算法描述 | 解释 |
|---|---|
| 前提 | 给定一个内含n个元素的有序数组A,满足A0<=A1<=A2<=·······<=An-1,一个待查值target |
| 1 | 设置left=0;right = n - 1 |
| 2 | 如果left > right ,结束查找,没找到 |
| 3 | 设置mid = (left + right )/2,mid为中间索引 |
| 4 | 如果target < Am,设置right = mid -1,跳到第2步 |
| 5 | 如果target > Am,设置left = mid +1,跳到第2步 |
| 6 | 如果Am = target,结束查找,找到了 |
算法实现
public int binarySearch(int[] arr,int target) {
int left = 0;
int right = arr.length-1;
while(left<=right) {
int mid = (left+right)>>>1;
if(target < arr[mid]) {
right = mid - 1;
}
else if (arr[mid] < target) {
left = mid + 1;
}
else {
return mid;
}
}
return -1;
}
注解:
1.为什么while循环条件是left<=right,而不是left<right?
因为当left=right时,mid=left=right可能为我们想要查找的值
2.为什么mid = (left+right)>>>1,而不是(left+right)/2呢? >>>是无符号右移,无符号右移一位相当于除2取整。 不用(left+right)/2原因是,当left+right的值超过int类型的正整数最大范围,其值就会由正变负
在其他的资料中二分查找与这个代码不一样,
✈️ 二分查找的改动版
public static int binarySearch1(int[] arr,int target) {
int left=0;
int right = arr.length; //第一处改动
while(left < right) { //第二处改动
int mid = (left+right)>>>1;
if(target < arr[mid]) {
right = mid; //第三处改动
}
else if (arr[mid] < target) {
left = mid + 1;
}
else {
return mid;
}
}
return -1;
}
⛵️注解:
right=arr.length,作为一个边界存在,left可能为我们的查找目标,但是right一定不是我们要找到的目标
?图解演示:
查找13
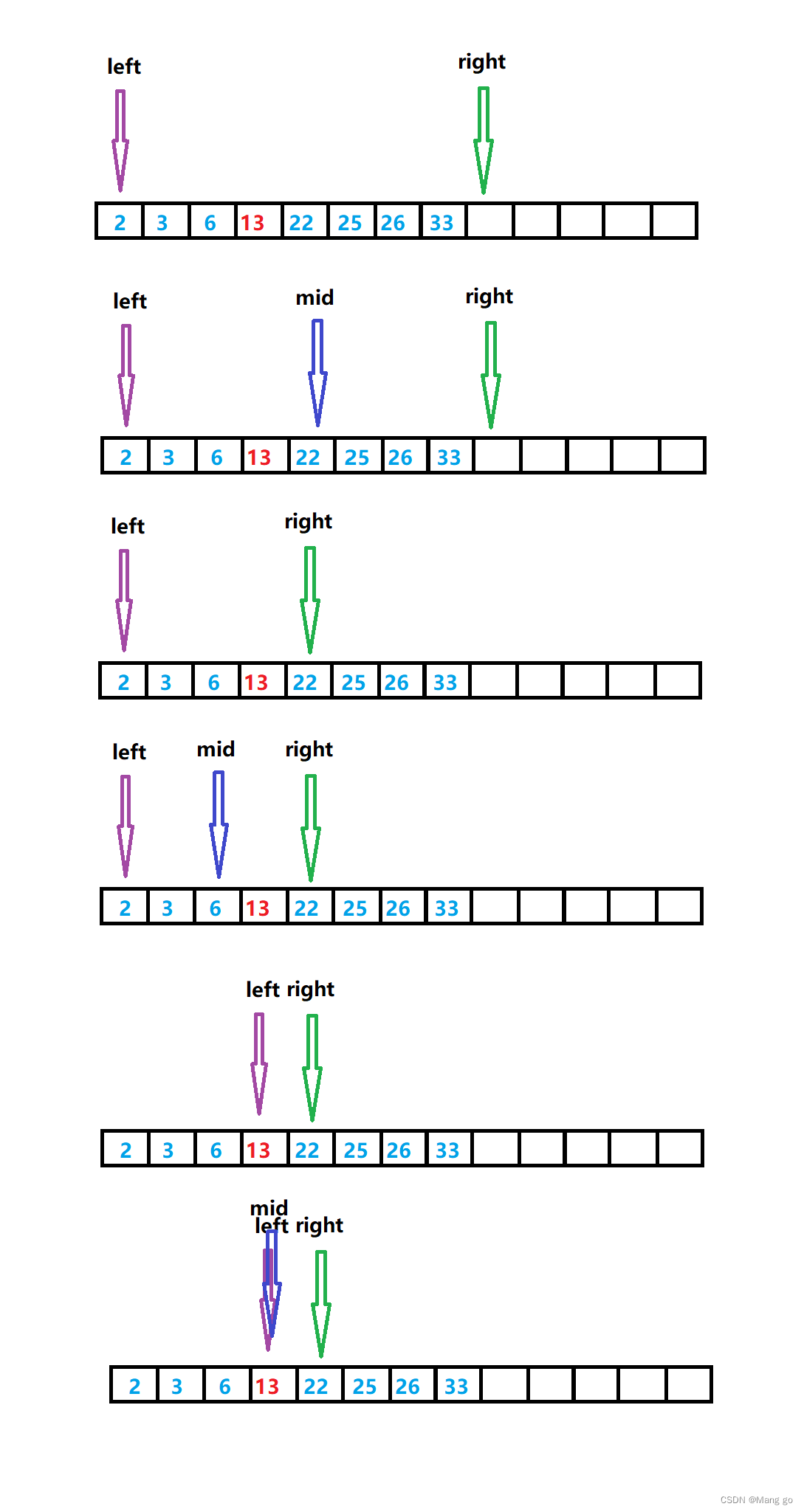
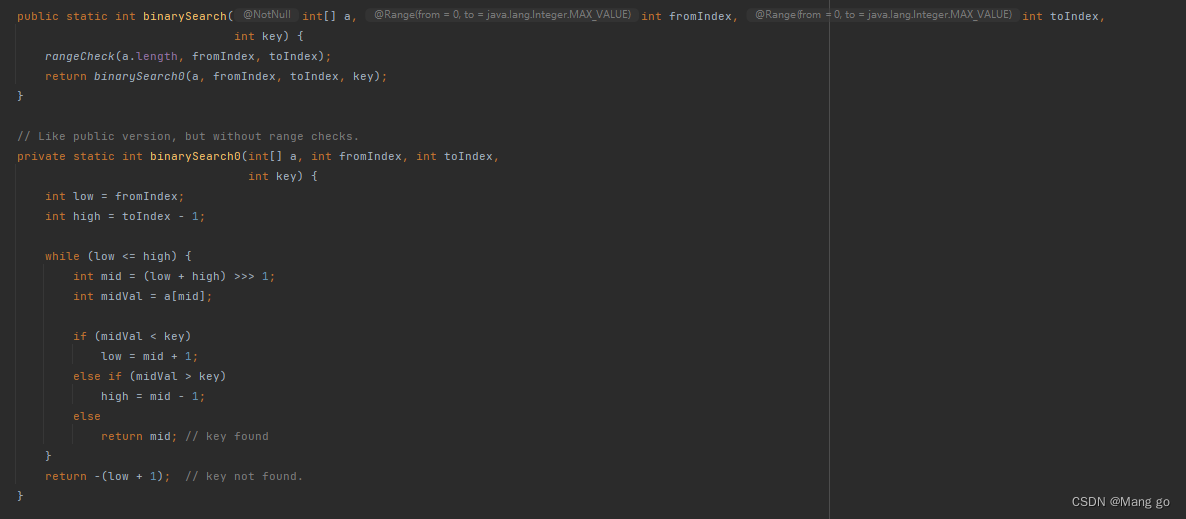
⛽️在Java中其实已经提供了二分查找的方法binarySearch
public class Test {
public static void main(String[] args) {
int[] arr ={1,2,3,4,5,5,6};
int target = Arrays.binarySearch(arr,3);
System.out.println(target);
}
}
?运行结果:
2
?二分查找对重复元素的处理
?重复元素最靠右的元素
说明:查找元素为重复元素的话,会查找到最右边的重复元素
Returns:
找到则返回最靠右索引
找不到返回-1
//重复元素最靠右的元素
public class Test5 {
public static int binarySearch2(int[] arr,int target) {
int left = 0;
int right = arr.length-1;
int cand = -1;
while (left <= right) {
int mid = (left + right)>>>1;
if(target < arr[mid]) {
right = mid-1;
} else if (arr[mid] < target) {
left = mid+1;
}
else {
cand = mid;
left = mid+1;
}
}
return cand;
}
}
说明:返回<=target的最右边的索引
Returns:
找到则返回最靠右索引
找不到返回小于target最右边的索引
public static int binarySearchRightMost(int[] arr,int target){
int left = 0;
int right = arr.length-1;
while(left <= right) {
int mid = (left + right )>>>1;
if(target < arr[mid]){
right = mid-1;
}
else {
left = mid + 1;
}
}
return left-1;
}
?重复元素最靠左的元素
说明:查找元素为重复元素的话,会查找到最左边的重复元素
Returns:
找到则返回最靠左索引
找不到返回-1
public static int binarySearch2(int[] arr,int target) {
int left = 0;
int right = arr.length-1;
int cand = -1;
while (left <= right) {
int mid = (left + right)>>>1;
if(target < arr[mid]) {
right = mid-1;
} else if (arr[mid] < target) {
left = mid+1;
}
else {
cand = mid;
right = mid - 1;
}
}
return cand;
}
说明:
返回>=target最左边的索引
Returns:
找到则返回最靠左索引
找不到返回比target大的最左边索引
public static int binarySearchLeftMost(int[] arr,int target) {
int left=0;
int right = arr.length-1;
while(left <= right) {
int mid = (left + right)>>>1;
if(target <= arr[mid]) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return left;
}
图解:
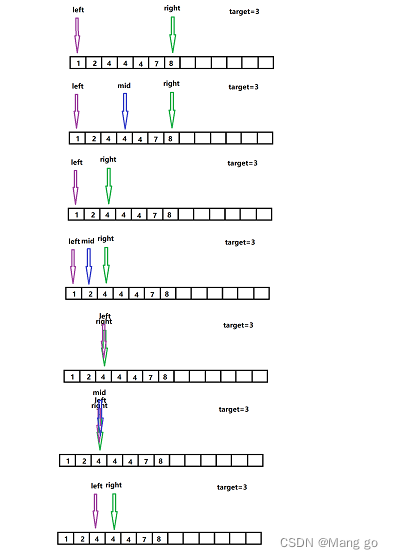
?leetcode二分查找题
1️⃣1.给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
⏩ 链接: 二分查找
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999,9999]之间。
class Solution {
public int search(int[] nums, int target) {
int i=0;
int j = nums.length-1;
while(i<=j){
int m=(i+j)>>>1;
if(target<nums[m]){
j=m-1;
}
else if(nums[m]<target){
i=m+1;
}
else{
return m;
}
}
return -1;
}
}
2️⃣2.给定一个排序的整数数组 nums 和一个整数目标值 target ,请在数组中找到 target ,并返回其下标。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
⏩ 链接: 搜索插入位置
class Solution {
public int searchInsert(int[] nums, int target) {
int left=0;
int right = nums.length-1;
while(left <= right) {
int mid = (left + right)>>>1;
if(target <= nums[mid]) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return left;
}
}
3️⃣3.给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
⏩ 链接: 在排序数组中查找元素的第一个和最后一个位置
class Solution {
public int[] searchRange(int[] nums, int target) {
int x=left(nums,target);
if(x==-1){
return new int[]{-1,-1};
}
else{
return new int[]{x,right(nums,target)};
}
}
public int left(int[] nums,int target) {
int i=0;
int j=nums.length-1;
int cand=-1;
while(i<=j){
int m=(i+j)>>>1;
if(target<nums[m]){
j=m-1;
}
else if(nums[m]<target){
i=m+1;
}
else{
cand=m;
j=m-1;
}
}
return cand;
}
public int right(int[] nums,int target) {
int i=0;
int j=nums.length-1;
int cand=-1;
while(i<=j){
int m=(i+j)>>>1;
if(target<nums[m]){
j=m-1;
}
else if(nums[m]<target){
i=m+1;
}
else{
cand=m;
i=m+1;
}
}
return cand;
}
}