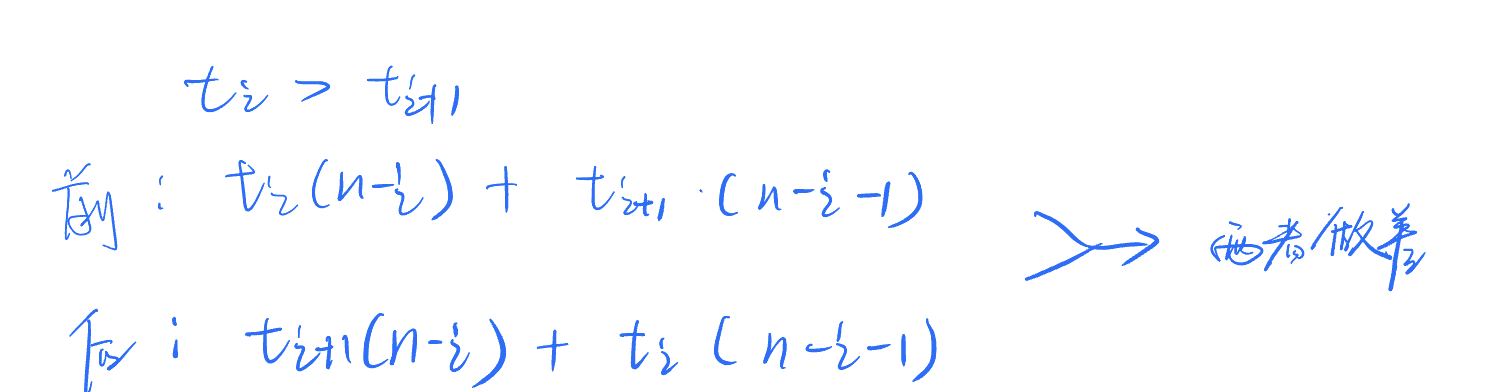一、Huffman树
- 哈夫曼树又称最优二叉树,是一种带权路径长度最短的二叉树,且为完全二叉树。
-
- 所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为0层,叶结点到根结点的路径长度为叶结点的层数)。
-
- 树的带权路径长度记为WPL=(W1L1+W2L2+W3L3+…+WnLn),N个权值Wi(i=1,2,…n)构成一棵有N个叶结点的二叉树,相应的叶结点的路径长度为Li(i=1,2,…n)。
-
- 贪心思想:
-
1、题目内容——合并果子

2、算法思路
(1)“合并果子”中的Huffman树
- 叶子结点为我们要进行合并的节点
- 合并代价为下方两个“代价总和”相加
-
从下向上开始合并
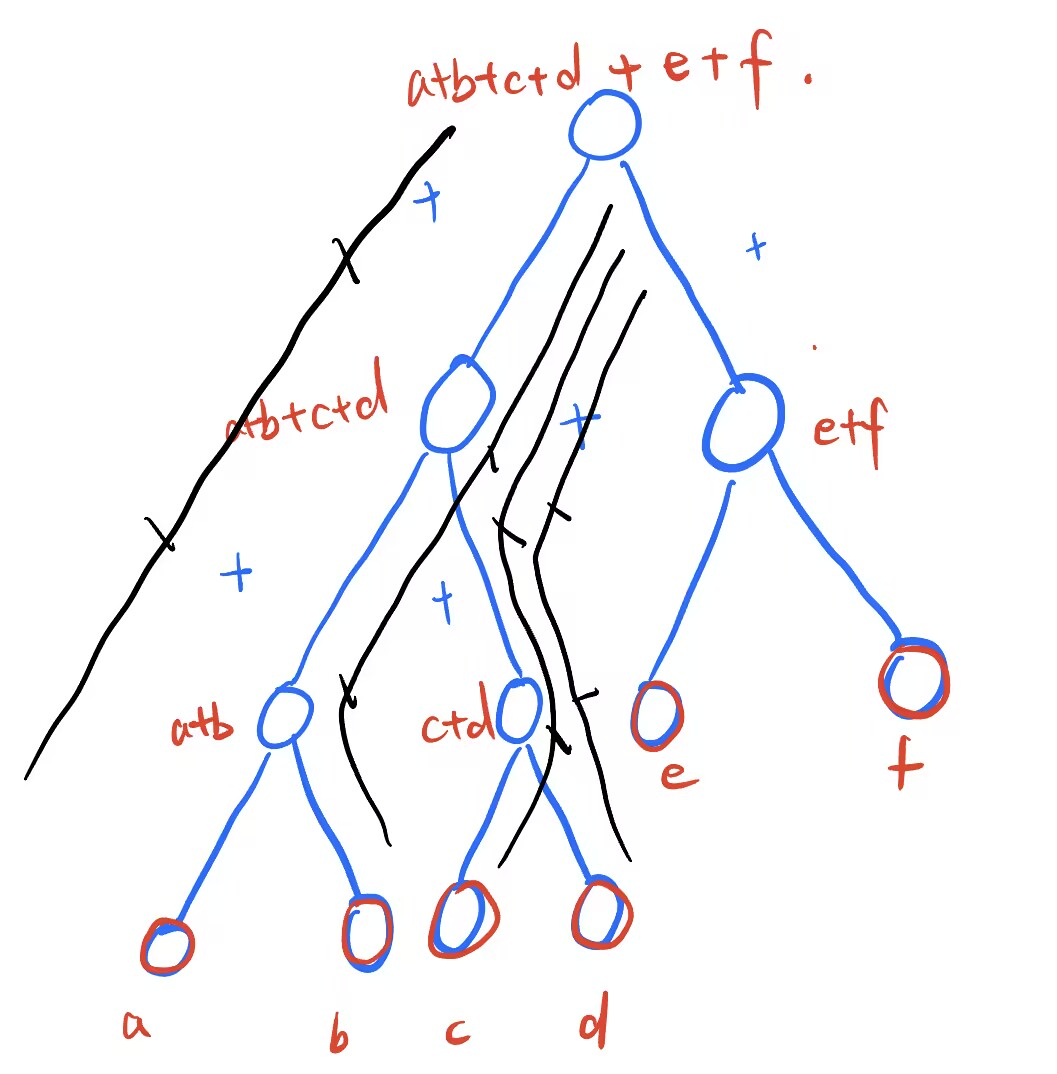
- 总和:(a + b)+ (c + d) +(a + b + c + d ) + e + f + a +b + c + d + e + f
- 优化:直接计算当前根节点到根节点距离
-
- 3a(到根节点的距离) + 3b + 3c + 3d + 2e + 2f
(2)算法步骤
-
方法: 每次选出最小的两堆进行合并,寻找局部最优解的过程
-
- 数最小的两个点,在树中一定是深度最深的,可以互为兄弟(不一定非得是兄弟节点)
-
- 数最小,但并未在最深的一层,则需要交换,这样将使整体权值变小(2f + 3b + -(3f + 2b) = b - f > 0)
(3)状态转移
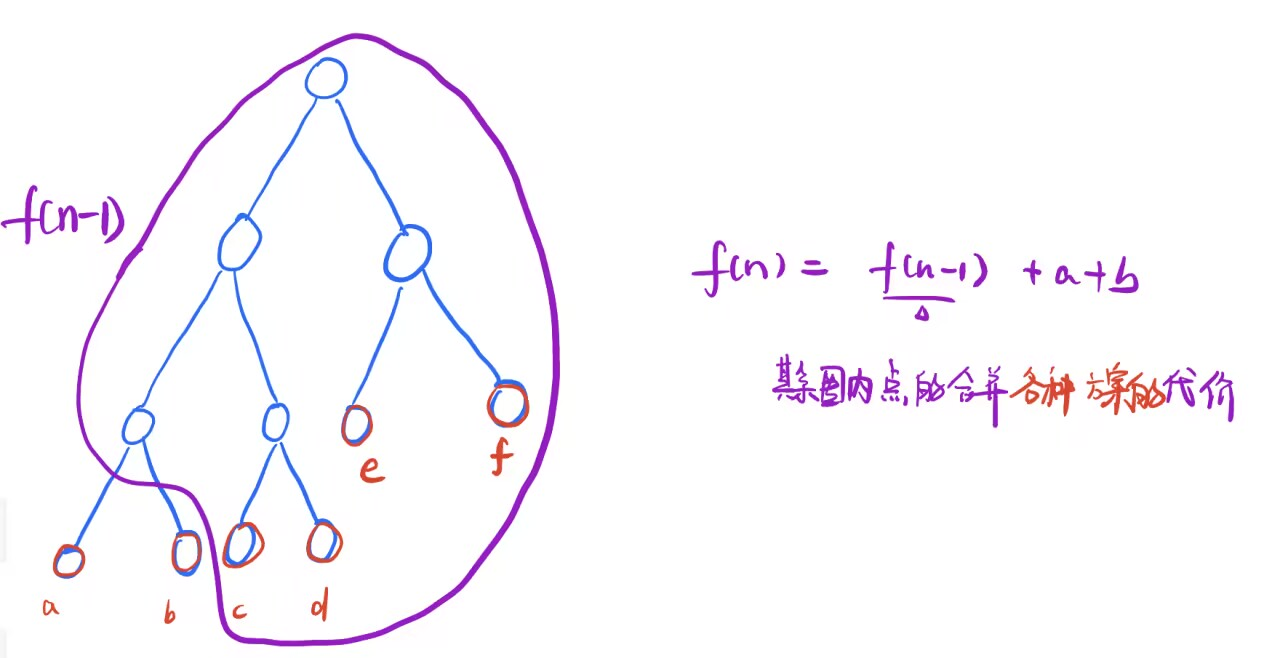
3、题解
import java.util.*;
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
Queue<Integer> heap = new PriorityQueue<>();
String str1 = in.readLine();
int n = Integer.parseInt(str1);
String[] str2 = in.readLine().split(" ");
for(int i = 0; i < n; i++){
int x = Integer.parseInt(str2[i]);
heap.add(x);
}
int res = 0;
while(heap.size() > 1){
int a = heap.poll();
int b = heap.poll();
res += a + b;
heap.add(a + b);
}
System.out.println(res);
}
}
二、排序不等式
-
排队问题 + 排队代价,如何让总体代价最小
- 贪心思想:
-
1、题目内容——排队打水
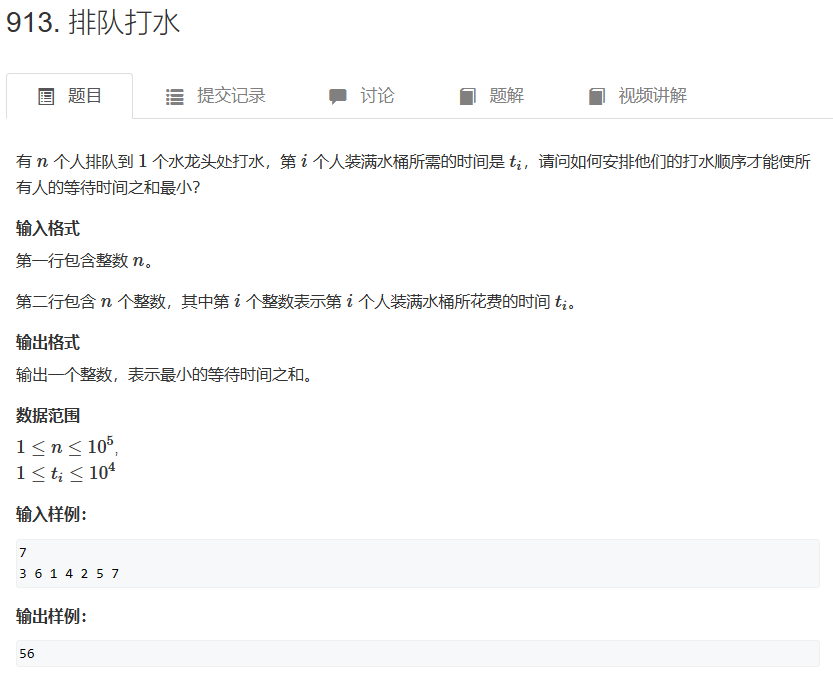
2、算法思路
(1)分析

(2)思路
(3)证明
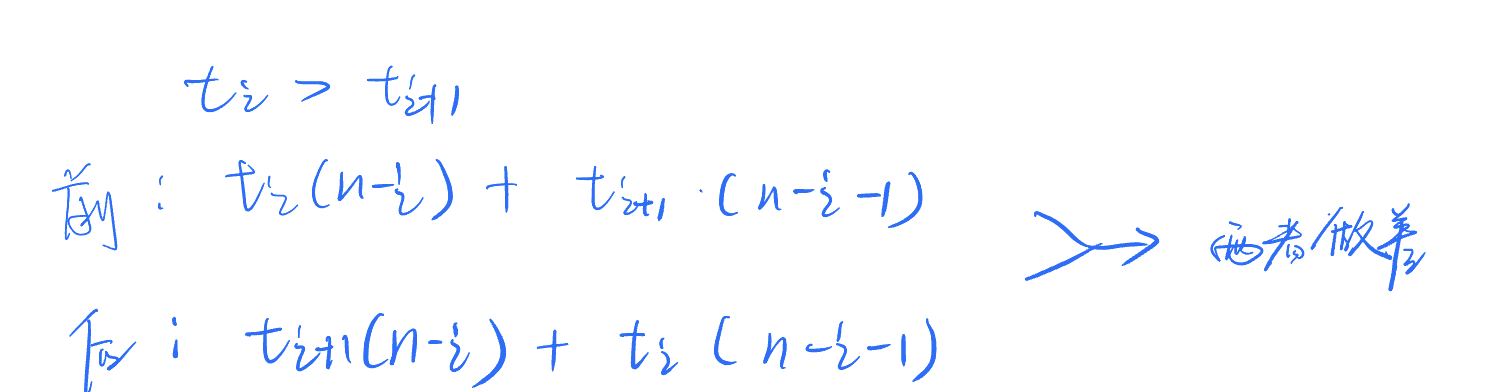
3、题解
import java.util.*;
import java.io.*;
public class Main{
static int N = 100010;
static int[] time = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String str1 = in. readLine();
int n = Integer.parseInt(str1);
String[] str2 = in.readLine().split(" ");
for(int i = 0; i < n; i++){
time[i] = Integer.parseInt(str2[i]);
}
Arrays.sort(time, 0 , n);
long res = 0;
for(int i = 0; i < n; i++){
res += time[i]*(n - i - 1);
}
System.out.println(res);
}
}