【力扣】319. 灯泡开关

题目：
初始时有 n 个灯泡处于关闭状态。第一轮，你将会打开所有灯泡。接下来的第二轮，你将会每两个灯泡关闭一个。

第三轮，你每三个灯泡就切换一个灯泡的开关（即，打开变关闭，关闭变打开）。第 i 轮，你每 i 个灯泡就切换一个灯泡的开关。直到第 n 轮，你只需要切换最后一个灯泡的开关。

找出并返回 n 轮后有多少个亮着的灯泡。

示例 1：

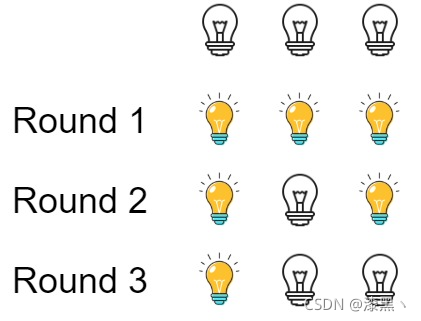
输入：n = 3
输出：1
解释：
初始时, 灯泡状态 [关闭, 关闭, 关闭].
第一轮后, 灯泡状态 [开启, 开启, 开启].
第二轮后, 灯泡状态 [开启, 关闭, 开启].
第三轮后, 灯泡状态 [开启, 关闭, 关闭].

你应该返回 1，因为只有一个灯泡还亮着。

示例 2：

输入：n = 0
输出：0

示例 3：

输入：n = 1
输出：1

提示：

0 <= n <= 109

答案：

class Solution {
    public int bulbSwitch(int n) {
        /**
         * 初始有n个灯泡关闭
        * 第i轮的操作是每i个灯泡切换一次开关（开->闭，闭->开），即切换i的倍数位置的开关。
        * 求n轮后亮着的灯泡？
        * （1）第i轮时，被切换的灯泡位置是i的倍数。
        * （2）由（1）得出，对于第p个灯泡来说，只有其第“因子”轮才会切换，若其有q个因子，则最终被切换q次。因为初始状态是关闭状态，那么因子数是奇数的灯泡最终是亮着的。
        * （3）只有平方数的因子个数不是成对出现，举例：4=1*4,2*2，其因子是1,2,4。
        * （4）那么题目最终转化为1~n里平方数的个数，进而转化为对n开平方根，向下取整即可。
         */
         return (int)Math.floor(Math.sqrt(n));
    }
}